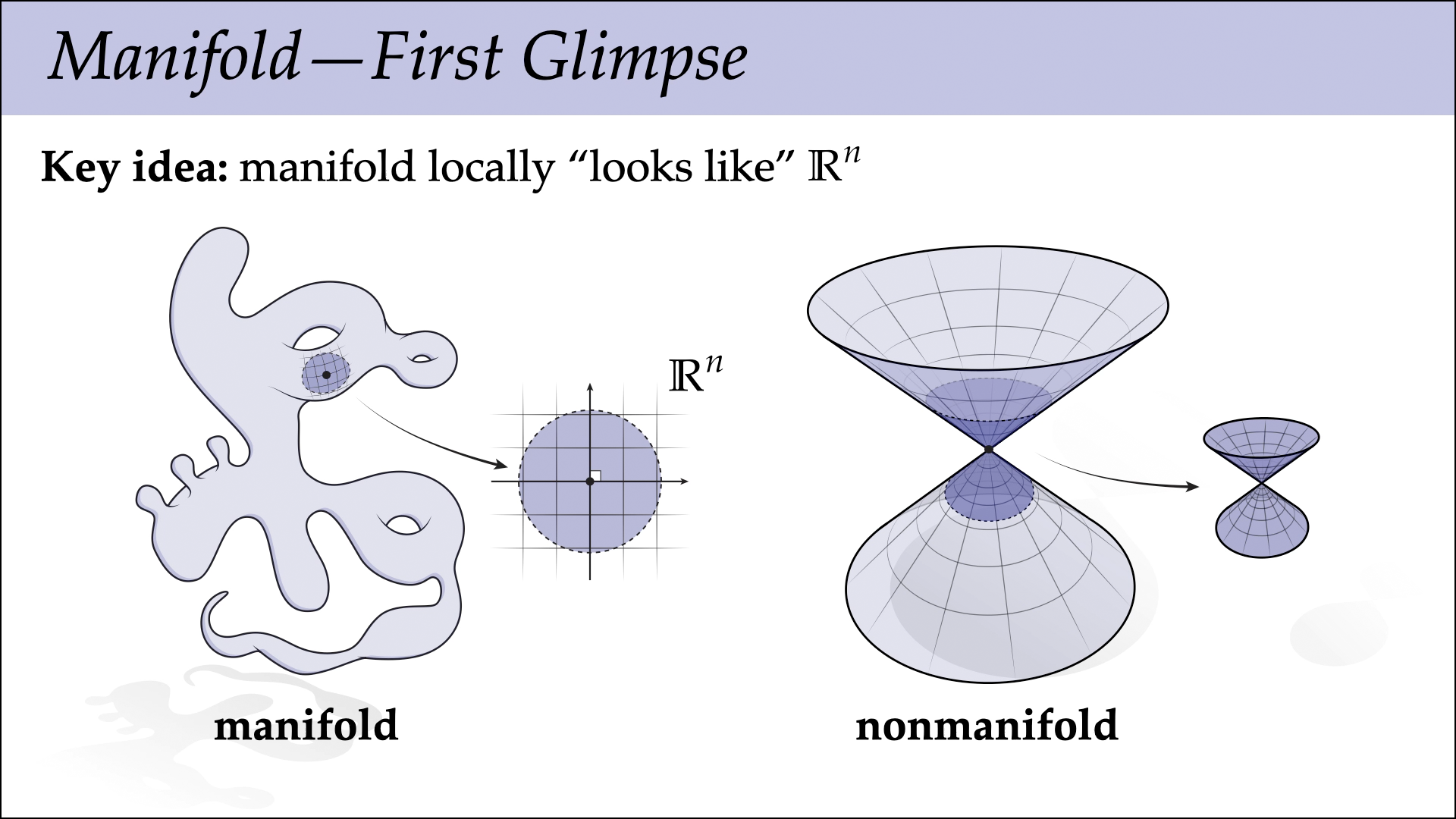
In tomorrow’s lecture we will catch a first glimpse of the idea of manifolds, which are pretty central to differential geometry. Rather than giving a formal definition in the smooth case, we’ll introduce a notion of discrete manifolds that capture the most important ideas. These discrete manifolds build on the idea of a simplicial complex, introduced in the previous lecture.

If two bodies are interacting with a common face, as it happens in many surface tension related phenomena, then in that condition 3 facets meet at a single edge. There exist many such edges and make something called three-phase-contact line. Can we call this complex as manifold? Can we apply all the tools that you are discussing in currently uploaded lectures?
I have used Ken Brakke’s Surface Evolver so my question is based on that experience.