The written portion of assignment 1 covers some of the most fundamental tools from exterior calculus, which we’ll be using extensively in our class and in future assignments. Initially this assignment may look a bit intimidating, but the homework is not as long as it might seem: all the text in the big gray blocks contains supplementary, formal definitions that you do not need to know in order to complete the assignments. Finally, don’t be shy about asking us questions here in the comments, via email, or during office hours.  We want to help you succeed on this assignment, so that you can enjoy all the adventures yet to come…

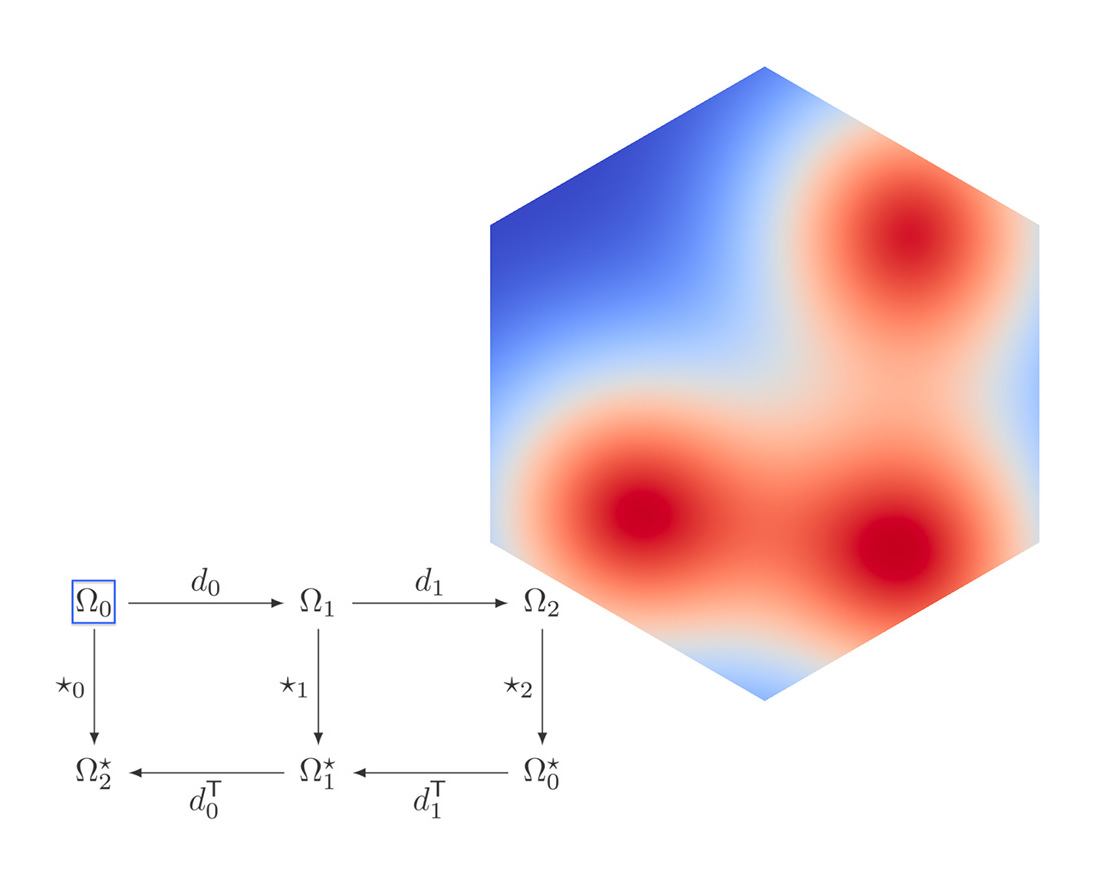
For the coding portion of your first assignment, you will implement the discrete exterior calculus (DEC) operators \(\star_0, \star_1, \star_2, d_0\) and \(d_1\). Once implemented, you will be able to apply these operators to a scalar function (as depicted above) by pressing the “\(\star\)” and “\(d\)” button in the viewer. The diagram shown above will be updated to indicate what kind of differential k-form is currently displayed. These basic operations will be the starting point for many of the algorithms we will implement throughout the rest of the class; the visualization (and implementation!) should help you build further intuition about what these operators mean and how they work Getting Started

• For this assignment, you need to implement the following routines:
  1. in core/geometry.[js/cpp]
     1. cotan
     2. barycentricDualArea
  2. in core/discrete-exterior-calculus.[js/cpp]
     1. buildHodgeStar0Form
     2. buildHodgeStar1Form
     3. buildHodgeStar2Form
     4. buildExteriorDerivative0Form
     5. buildExteriorDerivative1Form

In practice, a simple and efficient way to compute the cotangent of the angle \(\theta\) between two vectors \(u\) and \(v\) is to use the cross product and the dot product rather than calling any trigonometric functions directly; we ask that you implement your solution this way. (Hint: how are the dot and cross product of two vectors related to the cosine and sine of the angle between them?) Note that the barycentric dual area \(b_i\) associated with a vertex \(i\) is equal to one-third the area of all triangles \(ijk\) touching \(i\), i.e., \[ b_i := \frac{1}{3}\sum_{ijk} A_{ijk}, \] where the sum is taken over all triangles \(ijk\) containing vertex \(i\), and \(A_{ijk}\) is the area of triangle \(ijk\). Also, you can and should compute the ratio of dual edge lengths to primal edge lengths using the cotan formula (rather than finding the triangle circumcenters explicitly), which can be found in both the Discrete Exterior Calculus lecture, and in exercise 36 of the notes (though you don’t have to do the exercise for this homework). Handin instructions can be found in the Assignments section of the main page.