Lecture 2—Combinatorial Surfaces

Slides (PDF)

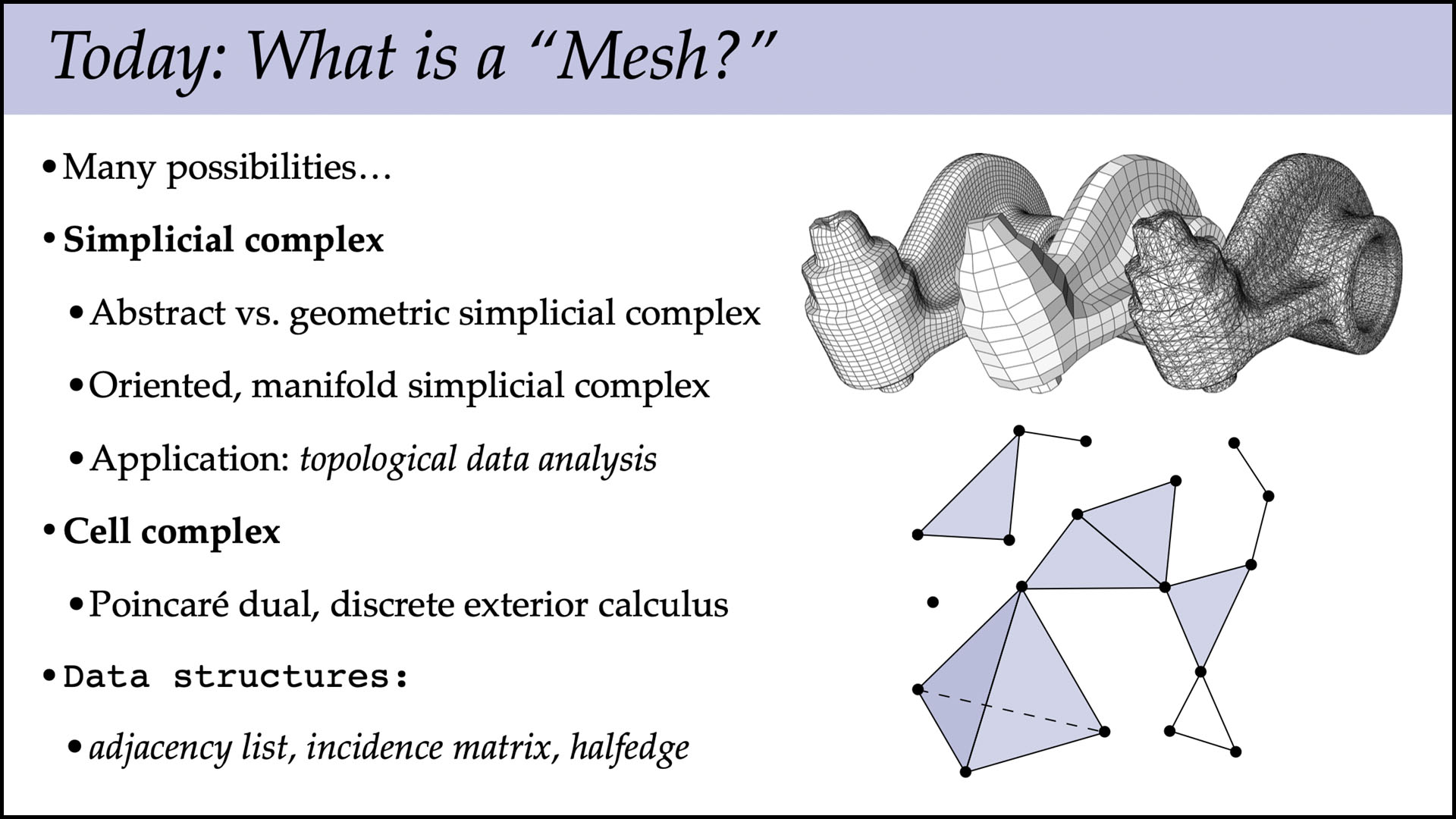
This lecture gives one precise definition to the notion of a “mesh,” namely a simplicial complex.  If we consider only the connectivity of a simplicial complex, rather than any locations for its vertices in space, we get an abstract simplicial complex.  From the perspective of differential geometry, an abstract simplicial complex plays the role of a so-called topological space, telling us how the domain is “connected up,” without saying anything specific about its geometry.