Lecture 2B—Introduction to Manifolds

Slides (PDF)

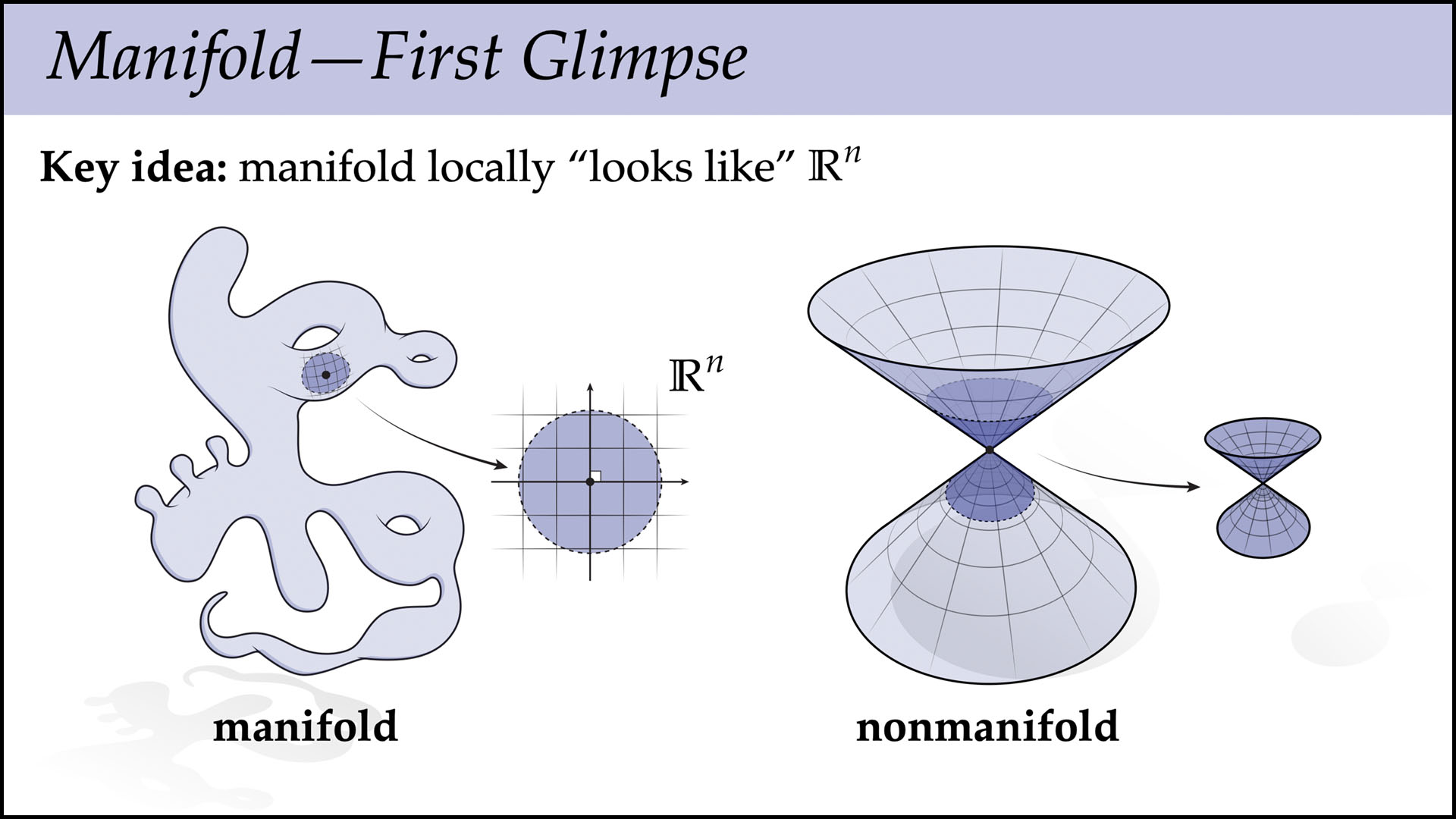
In this lecture we connect what we learned on the discrete side last time, about combinatorial surfaces and the simplicial complex, to manifolds, which are a central object in differential geometry. Manifolds are, very roughly speaking, a “particularly nice kind of (topological) space,” where concepts like “the neighborhood around a point” are always well-defined, and always look the same. By imposing an additional regularity condition on simplicial complexes, we likewise get a simplicial manifold, which more informally can be thought of as a “particularly nice kind of mesh.” In terms of practical algorithms, it’s often useful to assume manifold input, because it allows you to write code without worrying about tricky special cases.