Author: Keenan

Lecture 2—Combinatorial Surfaces


Slides (PDF)

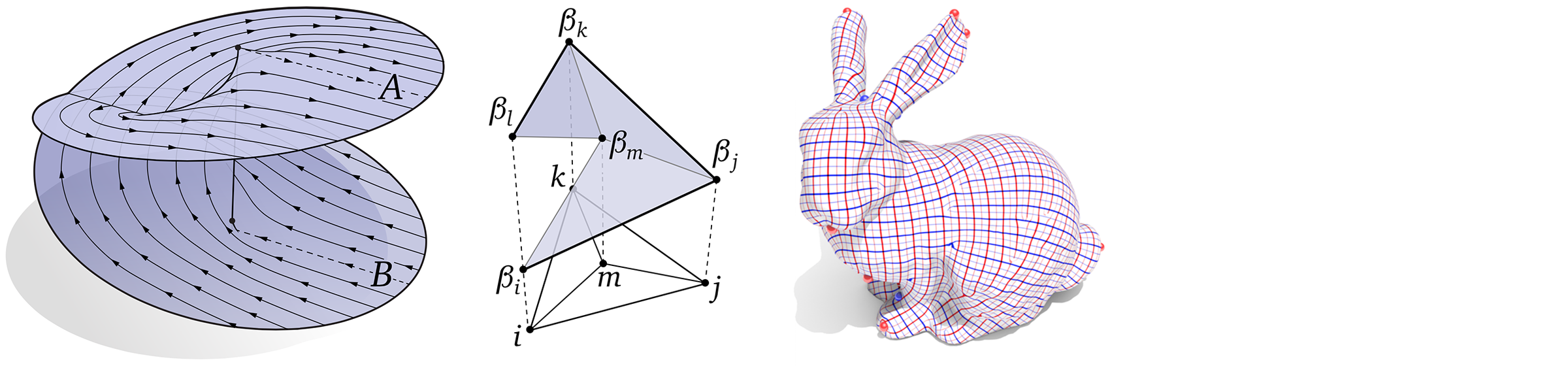
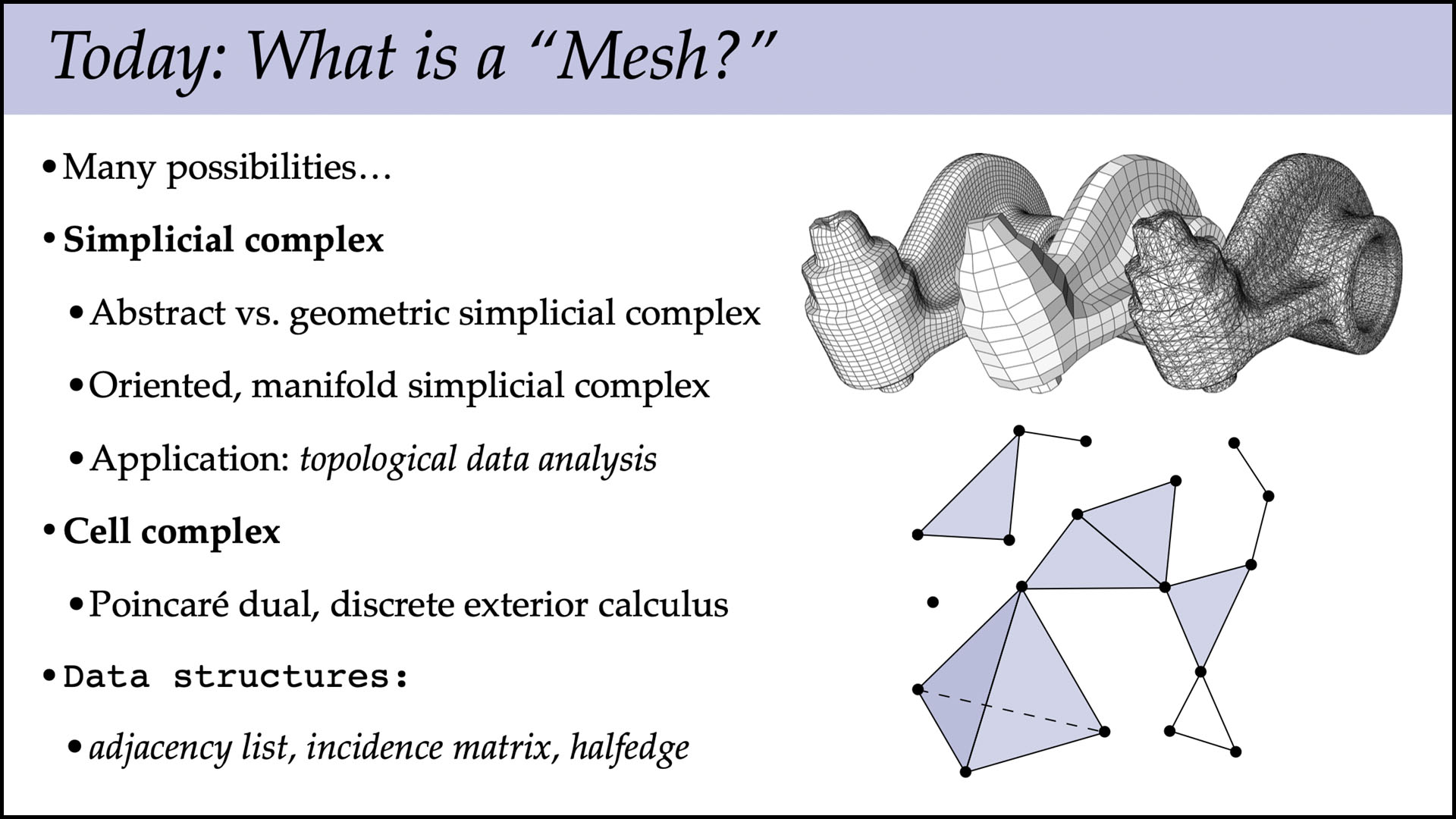
This lecture gives one precise definition to the notion of a “mesh,” namely a simplicial complex.  If we consider only the connectivity of a simplicial complex, rather than any locations for its vertices in space, we get an abstract simplicial complex.  From the perspective of differential geometry, an abstract simplicial complex plays the role of a so-called topological space, telling us how the domain is “connected up,” without saying anything specific about its geometry.

Reading 1: Overview of DDG (Due 1/25)

Your first reading assignment will be to read an overview article on Discrete Differential Geometry. Since we know we have a diverse mix of participants in the class, you have several options (pick one):

  1. (pages 1–3) Crane & Wardetzky, “A Glimpse into Discrete Differential Geometry”.
    This article discusses the “no free lunch” story about curvature we looked at in class, plus a broader overview of the field.
  2. (pages 1–5) Pottman et al, “Architectural Geometry”.
    This article discusses the beautiful tale of how discrete differential geometry is linked to modern approaches to computational design for architecture, as well as fabrication and “rationalization” of free-form designs.
  3. (pages 5–9) Bobenko & Suris, “Discrete Differential Geometry: Consistency As Integrability”.
    This article provides another overview of discrete differential geometry, with an emphasis on nets and their connection to the notion of integrability in geometry and physics.

Though written for a broad audience, be warned that all of these articles are somewhat advanced—the goal here is not to understand every little detail, but rather just get a high-level sense of what DDG is all about.

Assignment: Pick one of the readings above, and write 2–3 sentences summarizing what you read, plus at least one question about something you didn’t understand, or some thought/idea that occurred to you while reading the article.  For this first assignment, we are also very interested to know a little bit about YOU! E.g., why are you taking this course?  What’s your background?  What do you hope to get out of this course?  What are your biggest fears about the course?  Etc.

Handin instructions can be found in the “Readings” section of the Assignments page.  Note that you must send your summary in no later than 10am Eastern on the due date (January 25, 2024).  For readings, there is no credit for late work.

Enjoy!

Assignment -1: Favorite Formula

Part of your course grade is determined by participation, which can include both in-class participation as well as discussion here on the course webpage.  Therefore, your first assignment is to:

  1. create an account, and
  2. leave a comment on this post containing your favorite mathematical formula (see below).
To make things interesting, your comment should include a description of your favorite mathematical formula typeset in $\LaTeX$.  If you don’t know how to use $\LaTeX$ this is a great opportunity to learn — a very basic introduction can be found here.  (And if you don’t have a favorite mathematical formula, this is a great time to pick one!)
 
(P.S. Anyone interested in hearing about some cool “favorite theorems” should check out this podcast.)

Welcome to Discrete Differential Geometry! (Spring 2024)

Welcome to the website for 15-458/858 (Discrete Differential Geometry).  Here you’ll find course notes, lecture slides, and homework (see links on the right).  [Note that the video above is from 2020—so you can ignore administrative details about remote instruction!]

If you are a student in the class, register now by clicking here!

To participate in the class, you must register using your Andrew (CMU) email address.

A few things to note:

  • You will be subscribed to receive email notification about new posts, comments, etc.
  • You can ask questions by leaving a comment on a post.  If you’re apprehensive about asking questions in public, feel free to register under a pseudonym.
  • Otherwise, please associate a picture to your profile by registering your email address at Gravatar.com—doing so will help us better recognize you in class!
  • You can include mathematical notation in your questions using standard $\LaTeX$ syntax.  For instance, when enclosed in a pair of dollar signs, an expression like dollar\int_M K dA = 2\pi\chidollar gets typeset as $\int_M K dA = 2\pi\chi$.
If you encounter any problems while trying to use the website, please contact the TA (listed under the course description).