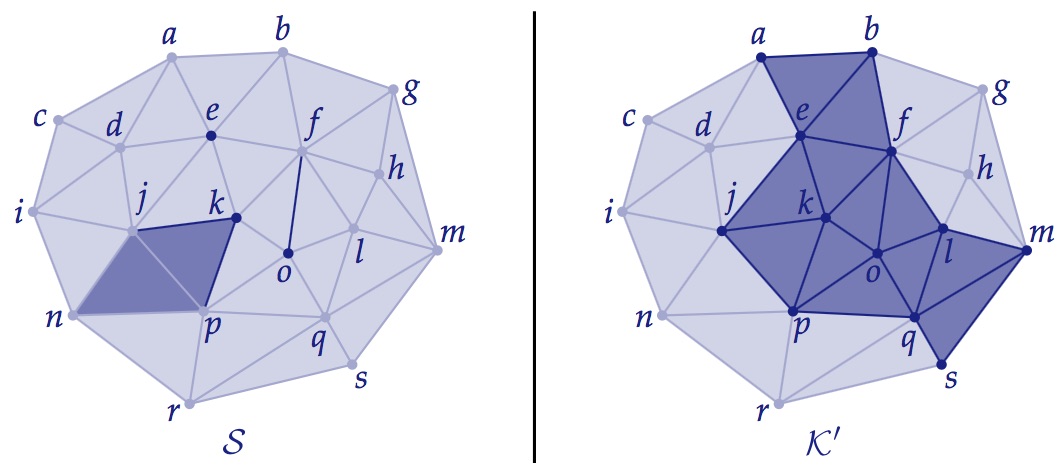
For the written part of your first homework you will do some exercises that will help familiarize you with basic descriptions and representations of combinatorial surfaces (simplicial surfaces, adjacency matrices, halfedge meshes), which will help prepare you to work with such surfaces as we continue through the course. (If any of this stuff seems abstract right now, don’t worry: we’ll use it over and over again to implement “real” algorithms starting in just a couple weeks!)
You must complete 8 out of 15 exercises in the Written Exercises section of Chapter 2 of the course notes. You may choose any set of 8 exercises you like, but if you do more than 8, please mark clearly on your submission which ones you would like us to grade.
The assignment is due on February 7, 2019 at 5:59:59pm Eastern (not at midnight!). Further hand-in instructions can be found on this page.
We made some minor fixes to the exercises in the course notes; grab a fresh copy of the PDF!
Is there a formal definition of a polygonal disk in the course notes? Or can Exercise 1 be done without it?
There’s not one in the course notes, but you can easily guess what it should be: roughly speaking, a polygonal disk is a topological disk made by gluing together polygons along their edges. Combinatorially, a polygon is just a collection of vertices with a circular ordering. An edge is still a pair of vertices. Like a simplicial disk, every edge of a polygon should be contained in either two polygons (on the interior) or one polygon (on the boundary). The polygons containing a given vertex should have either a single circular ordering (on the interior) or a single linear ordering (on the boundary), where two polygons can be adjacent in an ordering only if they share an edge.
That’s not formal, but hopefully it’s formal enough!
When doing exercise 13, using the definition as given in the book for a simplicial-1 requires us to know the triangulation of the 0-sphere. The 0-sphere is just the points -1 and 1 on the real line. So is the triangulation of the 0-sphere just two vertices?
Yes, exactly!
Are we allowed to use basic graph theory without proof?
Sure, but you really shouldn’t need anything too fancy.