Month: April 2019

Lecture 21—Geodesics

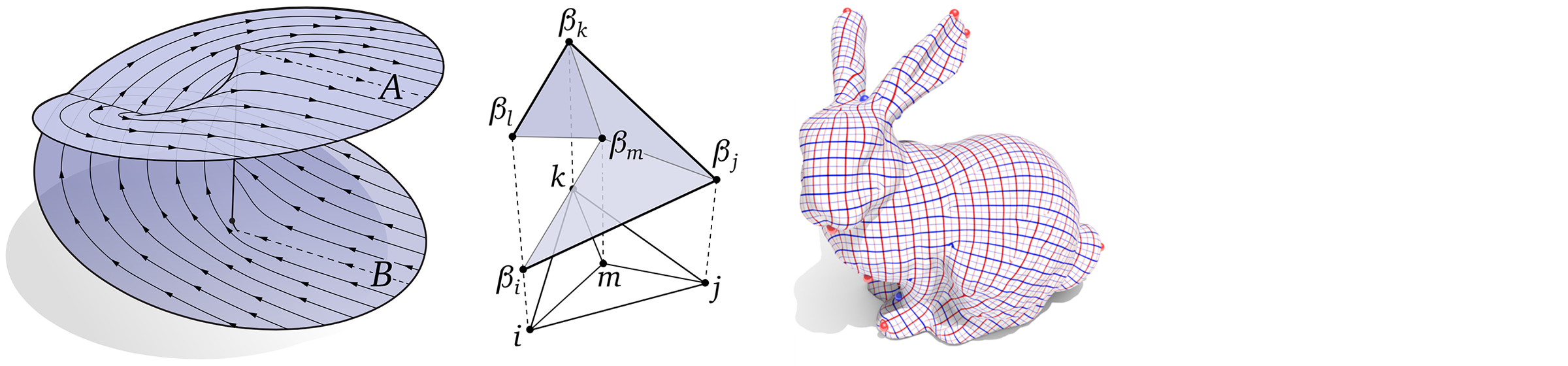
In this lecture we’ll start taking a look at geodesics, which generalize the concept of a “straight line” to curved manifolds. Here again we encounter The Game of discrete differential geometry: different characterizations of geodesics—namely, straightest vs. (locally) shortest—will lead us down a path toward different discrete analogues, and ultimately, different algorithms.

Assignment 5 [Written]: Geodesic Distance (Due 5/2)

Here’s the writeup for your second to last assignment. This time, we’re taking off the “training wheels” and having you read a real paper, rather than course notes. Why? Because you’re ready for it! At this point you have all the fundamental knowledge you need to go out into the broader literature and start implementing all sorts of algorithms that are built on top of ideas from differential geometry. In fact, this particular algorithm is not much of a departure from things you’ve done already: solving simple equations involving the Laplacian on triangle meshes. As discussed in our lecture on the Laplacian, you’ll find many algorithms in digital geometry processing that have this flavor: compute some basic data (e.g., using a local formula at each vertex), solve a Laplace-like equation, compute some more basic data, and so on.

Your main references for this assignment will be:

  • this video, which gives a brief (18-minute) overview of the algorithm, and
  • this paper, which explains the algorithm in detail.

Written exercises for this assignment are found below.


Warning: The original version of this assignment had an unsolvable linear system in Exercise 7. I updated the assignment on Thursday, so hopefully the exercise is possible now.

Assignment 5 [Coding]: Geodesic Distance (Due 5/2)

For the coding portion of this assignment, you will implement the heat method, which is an algorithm for computing geodesic distance on curved surfaces. All of the details you need for implementation are described in Section 3 of the paper, up through and including Section 3.2. Note that you need only be concerned with the case of triangle meshes (not polygon meshes or point clouds); pay close attention to the paragraph labeled “Choice of Timestep.”

Please implement the following routines in:

  1. projects/geodesic-distances/heat-method.js:
    1. constructor
    2. computeVectorField
    3. computeDivergence
    4. compute

Notes

  • Refer to sections 3.2 of the paper for discretizations of Algorithm 1 (page 3).
  • Recall that our Laplace matrix is positive semidefinite, which might differ from the sign convention the authors use.
  • The tests for computeVectorField and computeDivergence depend on the A and F matrices you define in your constructor. So if you fail the tests but your functions look correct, check whether you have defined the flow and laplace matrices properly.
  • Your solution should implement zero neumann boundary conditions (which are the “default behavior” of the cotan Laplacian) but feel free to tryout other Dirichlet and Neumann boundary conditions on your own.

Submission Instructions

Please rename your heat-method.js file to heat-method.txt and put it in a single zip file called solution.zip. This file and your solution to the written exercises should be submitted together in a single email to Geometry.Collective@gmail.com with the subject line DDG19A4.

Reading 7—Discrete Conformal Geometry (Due Thursday, April 18)

Your next reading will take a deep dive into conformal geometry and the many ways to discretize and compute conformal maps. This subject makes some beautiful and unexpected connections to other areas of mathematics (such as circle packings, and hyperbolic geometry), and is in some sense one of the biggest “success stories” of DDG, since there is now a complete uniformization theorem that mirrors the one on the smooth side. You’ll find out more about what this all means in the reading! The reading comes from the note, “Conformal Geometry of Simplicial Surface”:



For your assignment you will need to read the Overview (1.1) and Preliminaries (1.2); you must also pick one of Part I, Part II, or Part III to read, each of which covers a different perspective on discrete conformal maps. The most interesting subject, perhaps, is the connections to hyperbolic geometry in Part IV, which you can read for your own enjoyment! 🙂

Hand-in instructions are, as usual, found on the assignments page. The reading is due at 10 AM Eastern, before lecture on April 18, 2019.

Bonus Lecture: Simulation and Geometry

In this lecture, we saw some of the geometry underlying classical mechanics and explored how understanding this geometry can lead us to well-behaved simulation algorithms. Along the way, we explored conservation laws and Noether’s theorem.


Discrete Mechanics

You can find a demo of the different Euler integrators applied to a pendulum here, and you can find a demo of how they flow particles on phase space here.

Assignment 4 [Written]: Conformal Parameterization (Due 4/16)


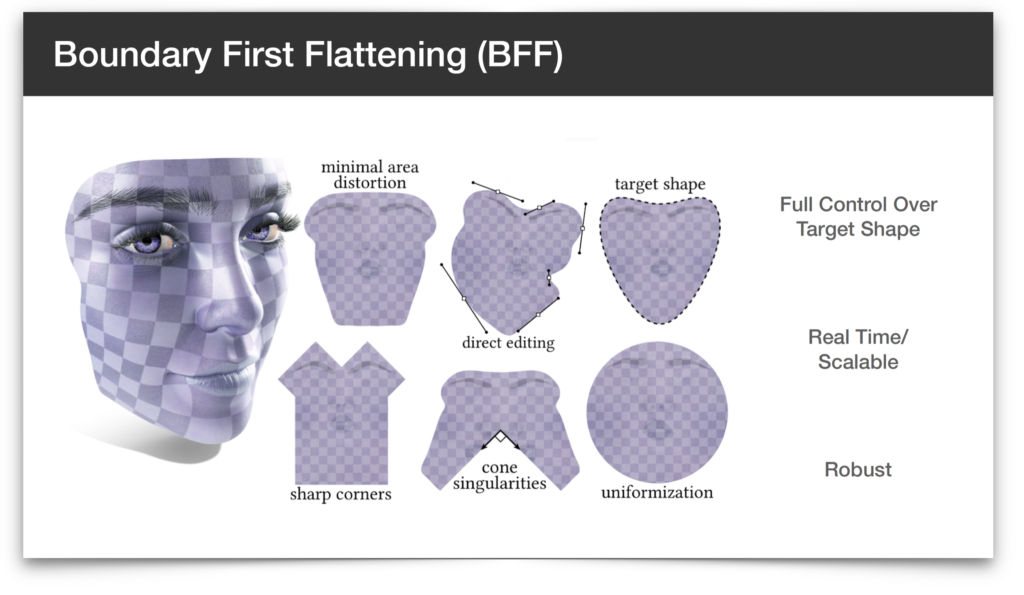
The written part of your next assignment, on conformal surface flattening, is now available below. Conformal flattening is important for (among other things) making the connection between processing of 3D surfaces, and existing fast algorithms for 2D image processing. You’ll have the opportunity to implement one of these algorithms in the coding part of the assignment.


Assignment 4

Assignment 4 [Coding]: Conformal Parameterization (Due 4/16)

For the coding portion of your assignment on conformal parameterization, you will implement the Spectral Conformal Parameterization (SCP) algorithm as described in the course notes.Please implement the following routines in

  1. core/geometry.js:
    1. complexLaplaceMatrix
  2. projects/parameterization/spectral-conformal-parameterization.js:
    1. buildConformalEnergy
    2. flatten
  3. utils/solvers.js:
    1. solveInversePowerMethod
    2. residual

Notes

  • I added a few tests for utils/solvers.js. They’re available in the git repository. If you’re familiar with git, you can pull the changes. If you’d prefer not to mess around with git, you can also just download the files and put them in tests/utils.
    • Warning: I fixed a problem with the residual test. In the notes, the residual is defined as a vector $Ax – \lambda x$. But your function residual should return a float. You should return $\frac{\|Ax – \lambda x\|_2}{\|x\|_2}$. Furthermore, you should compute $\lambda$ as $\frac{x^\dagger A x}{x^\dagger x}$ where $x^\dagger$ is the conjugate transpose of $x$.
  • The complex version of the cotan-Laplace matrix can be built in exactly the same manner as its real counterpart. The only difference now is that the cotan values of our matrix will be complex numbers with a zero imaginary component. This time, we will work with meshes with boundary, so your Laplace matrix will have to handle boundaries properly (you just have to make sure your cotan function returns 0 for halfedges which are in the boundary).
  • The buildConformalEnergy function builds a $|V| \times |V|$ complex matrix corresponding to the conformal energy $E_C(z) = E_D(z) – \mathcal A(Z)$ where $E_D$ is the Dirichlet energy (given by our complex cotan-Laplace matrix) and $\mathcal A$ is the total signed area of the region $z(M)$ in the complex plane (Please refer to Section 7.4 of the notes for more details). You may find it easiest to iterate over the halfedges of the mesh boundaries to construct the area matrix (Recall that the Mesh object has a boundaries variable which stores all the boundary loops.
  • The flatten function returns a dictionary mapping each vertex to a vector (linear-algebra/vector.js) of planar coordinates by finding the eigenvector corresponding to the smallest eigenvalue of the conformal energy matrix. You can compute this eigenvector by using solveInversePowerMethod (described below).
  • Your solveInversePowerMethod function should implement Algorithm 1 in Section 7.5 of the course notes with one modification – after computing $Ay_i = y_{i-1}$, center $y_i$ around the origin by subtracting its mean. You don’t have to worry about the $B$ matrix or generalized eigenvalue problem. Important: Terminate your iterations when your residual is smaller that 10^-10.
  • The parameterization project directory also contains a basic implementation of the Boundary First Flattening (BFF) algorithm. Feel free to play around with it in the viewer and compare the results to your SCP implementation.

Submission Instructions

Please rename your geometry.js, spectral-conformal-parameterization.js and solvers.js files to geometry.txt, spectral-conformal-parameterization.txt and solvers.txt (respectively) and put them in a single zip file called solution.zip. These files and your solution to the written exercises should be submitted together in a single email to Geometry.Collective@gmail.com with the subject line DDG19A4.

Lecture 20: Discrete Conformal Geometry

In this lecture we’ll attempt to translate several smooth characterizations of conformal maps into the discrete setting. We’ll also see how each of these attempts leads to a different class of computational algorithms, with different trade offs. Although conformal maps are often associated with angle preservation, we’ll see that preserving angles at the discrete level results in a theory that is far to rigid: i.e., it does not capture any of the interesting structure of smooth conformal geometry. Instead, we’ll see how less-obvious starting points (such as patterns of circles, or preservation of length cross ratios) lead to some deep and beautiful connections between the classic smooth picture, and the discrete, combinatorial picture.

Lecture 19: Conformal Geometry

A basic task in geometric algorithms is finding mappings between surfaces, which can be used to transfer data from one place to another. A particularly nice class of algorithms (both from a mathematical and computational perspective) are conformal mappings, which preserve angles between vectors, and are generally very well-behaved. In this lecture we’ll take a look at smooth characterizations of conformal maps, which will ultimately inspire the way we talk about conformal maps in the discrete/computational setting.