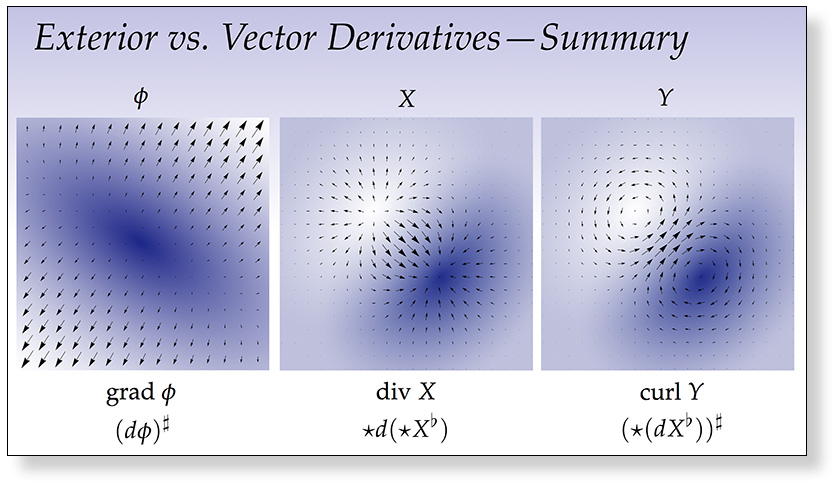
Ordinary calculus provides tools for understanding rates of change (via derivatives), total quantities (via integration), and the total change (via the fundamental theorem of calculus). Exterior calculus generalizes these ideas to \(n\)-dimensional quantities that arise throughout geometry and physics. Our first lecture on exterior calculus studies the exterior derivative, which describes the rate of change of a differential form, and (together with the Hodge star) generalizes the gradient, divergence, and curl operators from standard vector calculus.
Skip to content

CS 15-458/858: Discrete Differential Geometry
CARNEGIE MELLON UNIVERSITY | SPRING 2021 | TUE/THU 12:20-1:40 | Remote