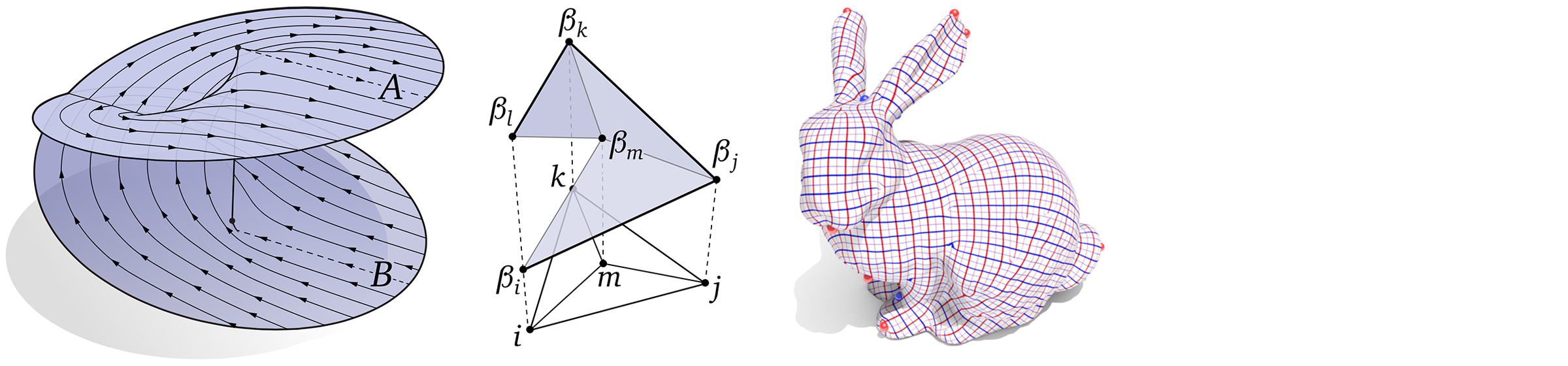
A basic task in geometric algorithms is finding mappings between surfaces, which can be used to transfer data from one place to another. A particularly nice class of mappings (both from a mathematical and computational perspective) are conformal maps, which preserve angles between vectors, and are generally very well-behaved. In this first lecture we’ll take a look at smooth characterizations of conformal maps, which will ultimately inspire the way we talk about conformal maps in the discrete/computational setting.
The video covering both today and Thursday’s lecture (on discrete aspects of conformal maps) can be found here.