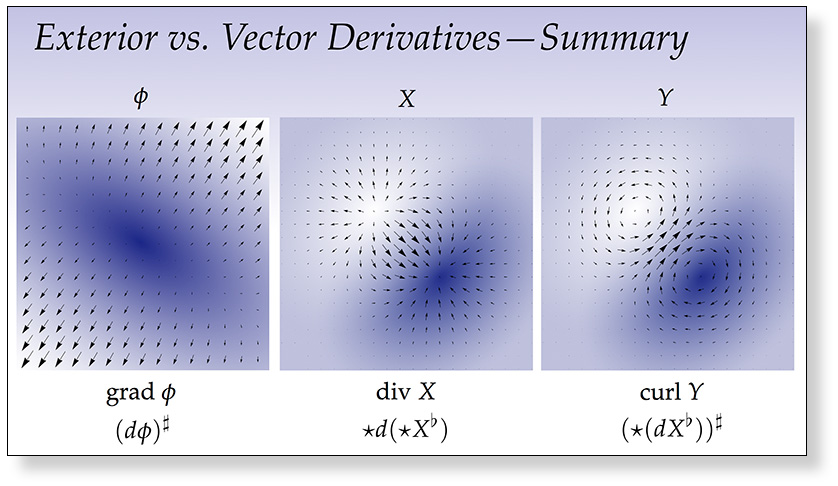
Ordinary calculus provides tools for understanding rates of change (via derivatives), total quantities (via integration), and the total change (via the fundamental theorem of calculus). Exterior calculus generalizes these ideas to \(n\)-dimensional quantities that arise throughout geometry and physics. Our first lecture on exterior calculus studies the exterior derivative, which describes the rate of change of a differential form, and (together with the Hodge star) generalizes the gradient, divergence, and curl operators from standard vector calculus.
Month: February 2024
Slides—Differential Forms in \(R^n\)
A differential \(k\)-form describes a \(k\)-dimensional measurement at each point of space. For instance, the area 2-form on a sphere tells us how much each little piece of the sphere should contribute to an integral over the sphere. In this lecture we give some basic facts and definitions about differential \(k\)-forms, and how to work with them in coordinates. Ultimately differential \(k\)-forms will pave the way to a general notion of integration, which in turn will be our basic mechanism for turning smooth equations into discrete ones (by integrating over elements of a mesh).
Reading 3: Exterior Algebra and k-Forms (due 2/8)
Your next reading assignment will help you review the concepts we’ve been discussing in class: describing “little volumes” or \(k\)-vectors using the wedge product and the Hodge star, and measuring these volumes using “dual” volumes called \(k\)-forms. These objects will ultimately let us integrate quantities over curved domains, which will also be our main tool for turning smooth equations from geometry and physics into discrete equations that we can actually solve on a computer.
The reading is Chapter 4, “A Quick and Dirty Introduction to Exterior Calculus”, up through section 4.5.1 (pages 45–65). It will be due Thursday, February 8 at 10am Eastern time. See the assignments page for handin instructions.
Your next homework will give you some hands-on practice with differential forms; just use this reading to get familiar with the basic concepts.