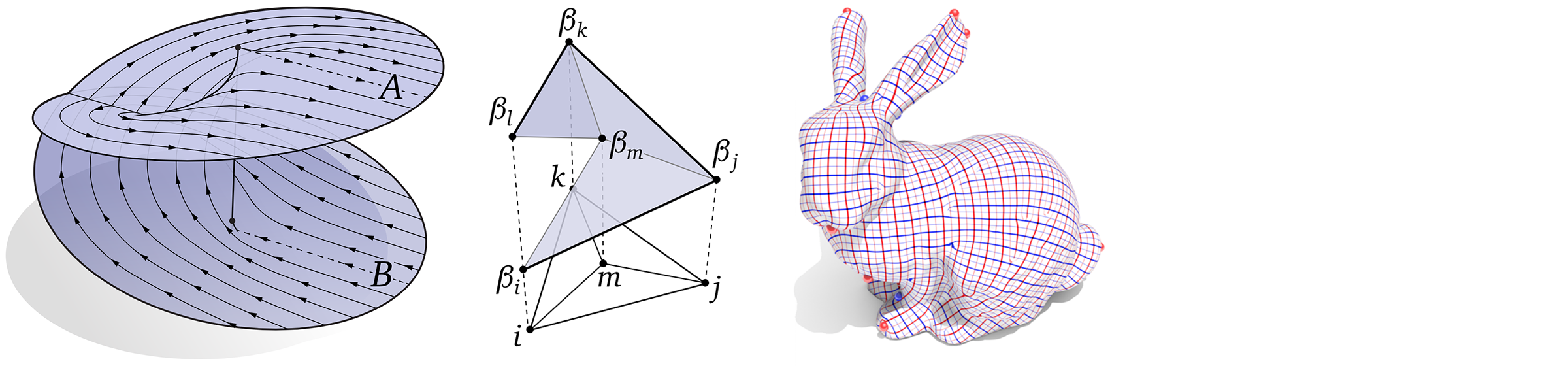
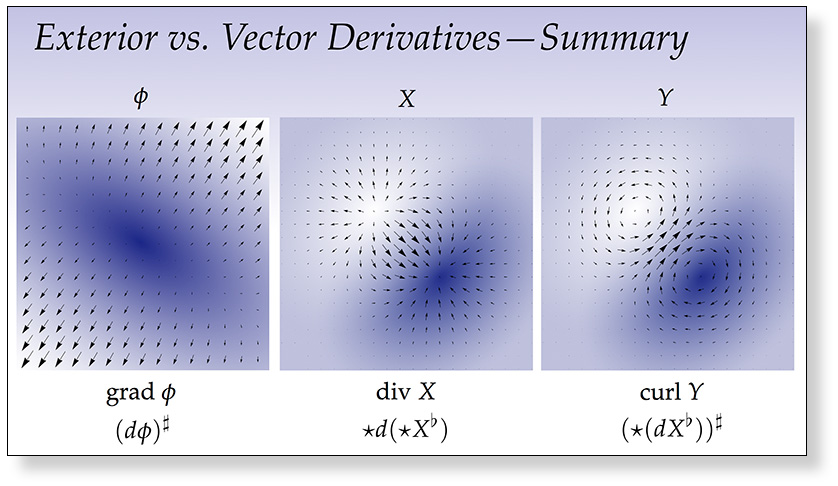
Ordinary calculus provides tools for understanding rates of change (via derivatives), total quantities (via integration), and the total change (via the fundamental theorem of calculus). Exterior calculus generalizes these ideas to \(n\)-dimensional quantities that arise throughout geometry and physics. Our first lecture on exterior calculus studies the exterior derivative, which describes the rate of change of a differential form, and (together with the Hodge star) generalizes the gradient, divergence, and curl operators from standard vector calculus.
Author: Keenan
Slides—Differential Forms in \(R^n\)
A differential \(k\)-form describes a \(k\)-dimensional measurement at each point of space. For instance, the area 2-form on a sphere tells us how much each little piece of the sphere should contribute to an integral over the sphere. In this lecture we give some basic facts and definitions about differential \(k\)-forms, and how to work with them in coordinates. Ultimately differential \(k\)-forms will pave the way to a general notion of integration, which in turn will be our basic mechanism for turning smooth equations into discrete ones (by integrating over elements of a mesh).
Reading 3: Exterior Algebra and k-Forms (due 2/8)
Your next reading assignment will help you review the concepts we’ve been discussing in class: describing “little volumes” or \(k\)-vectors using the wedge product and the Hodge star, and measuring these volumes using “dual” volumes called \(k\)-forms. These objects will ultimately let us integrate quantities over curved domains, which will also be our main tool for turning smooth equations from geometry and physics into discrete equations that we can actually solve on a computer.
The reading is Chapter 4, “A Quick and Dirty Introduction to Exterior Calculus”, up through section 4.5.1 (pages 45–65). It will be due Thursday, February 8 at 10am Eastern time. See the assignments page for handin instructions.
Your next homework will give you some hands-on practice with differential forms; just use this reading to get familiar with the basic concepts.
Slides—\(k\)-Forms
Today we continue our journey toward building up (discrete) exterior calculus by talking about how to measure little k-dimensional volumes. Just like rulers measure length, and cups measure volume, k-forms will be used to take measurements of the little k-dimensional volumes or k-vectors that we built up using exterior algebra in our previous lecture. Such measurements will ultimately allow us to talk about integration over curved spaces; in the discrete setting, these measurements will be the basic data we associate with the elements of mesh.
Recitation: Getting started with the coding assignments
Here is a nice recording of the recitation session from earlier years.
This serves as a review on the halfedge data structure, working with sparse matrices and solving linear systems.
Full video and slides are available here:
- Full video
- Concept review (0:00 – 16:58)
- Intro to ddg-exercises-js (16:58 – 23:22)
- Intro to ddg-exercises (C++) (23:22 – 31:41)
- Slides
Slides—Exterior Algebra
Today’s lecture will cover one of the basic tools we’ll use throughout the rest of the course: exterior algebra. The basic idea is to add a couple new operations to our usual list of vector operations (dot product, cross product, etc.) that make it easy to talk about volumes rather than just vectors. If you felt ok working with things like the cross product and the determinant in your linear algebra/vector calculus courses, this shouldn’t be too big of a leap. (If not, could be a good moment for a review!)
Assignment 0 (Coding): Combinatorial Surfaces

For the coding portion of your first assignment, you will implement some operations on simplicial complexes which were discussed in class and in Chapter 2 of the course notes. Once implemented, you will be able to select simplices and apply these operations to them by clicking the appropriate buttons in the viewer (shown above).
Getting Started
- Decide whether you want to use the web skeleton (in JavaScript) or the desktop skeleton (in C++). The web skeleton should “just work” for anyone with a web browser. Setting up the C++ skeleton is also fairly automatic (just a few git commands), but requires a little more familiarity with coding environments. (The benefit of the C++ version is that it’s built on a richer, real-world mesh processing/visualization library than the web version.)
- To use the JavaScript version, download or clone the files in the ddg-exercises-js repository.
- To use the C++ version, follow the instructions in the ddg-exercises repository. It is important that you follow the “Getting Started” instructions and do not simply git clone the repo. Otherwise, dependencies will not be installed correctly, and the code will not build. If you struggle to get the C++ version working on your platform, we recommend you switch to the JavaScript version.
- Either way, you should need to download just one code skeleton for the whole semester (though we may push periodic updates to fix bugs, etc.).
- For this assignment, you will need to implement the following routines in projects/simplicial-complex-operators/simplicial-complex-operators.[js|cpp]:
- assignElementIndices
- buildVertexEdgeAdjacencyMatrix
- buildEdgeFaceAdjacencyMatrix
- buildVertexVector
- buildEdgeVector
- buildFaceVector
- star
- closure
- link
- isComplex
- isPureComplex
- boundary
Notes
- The JavaScript assignment comes with a viewer projects/simplicial-complex-operators/index.html which lets you apply your operators to simplices of meshes and visualize the results. Likewise, the C++ version comes with a viewer with similar functionality. (Viewers will be available for all assignments throughout the semester.)
- Pay close attention to the course notes! Some routines really must be implemented with sparse matrices, not directly with the halfedge mesh data structure.
- Selecting simplices will not work until you fill in the assignElementIndices function.
- The assignment also comes with a test script tests/simplicial-complex-operators/text.html which you can use to verify the correctness of your operators.
- The web framework is implemented in Javascript, which means no compilation or installation is necessary on any platform. You can simply get started by opening the index.html file in projects/discrete-exterior-calculus/ in a web browser. We recommend using Chrome or Firefox. Safari has poor WebGL performance.
- If you do not have prior experience with Javascript, do not worry! You should be able to get a handle on Javascript syntax by reading through some of the code in the framework (a good place to start might be core/geometry.js). The framework also contains extensive documentation (see docs/index.html).
- All browsers come with tools for debugging (for instance the JavaScript Console in Chrome).
Submission Instructions
The assignment is due on the date listed on the calendar, at 5:59:59pm Eastern (not at midnight!). Further hand-in instructions can be found on this page.
Assignment 0 (Written): Combinatorial Surfaces

For the written part of your first homework you will do some exercises that will help familiarize you with basic descriptions and representations of combinatorial surfaces (simplicial surfaces, adjacency matrices, halfedge meshes), which will help prepare you to work with such surfaces as we continue through the course. (If any of this stuff seems abstract right now, don’t worry: we’ll use it over and over again to implement “real” algorithms starting in just a couple weeks!)
You must complete all 15 exercises from the Written Exercises section of Chapter 2 of the course notes. If these exercises seem scary and unfamiliar, and you don’t know where to start, that’s ok! This is not typical computer science stuff, and you shouldn’t necessarily know how to do it right off the bat. If you find yourself stumbling, please reach out to the instructor/TAs and your classmates on Piazza, Discord, or during the office hours/Q&A sessions. We’ll have you up and running in no time. 🙂
The assignment is due on the date listed on the calendar, at 5:59:59pm Eastern (not at midnight!). Hand-in instructions can be found on this page.
Reading 2: Combinatorial Surfaces (due Thu, Feb 1)
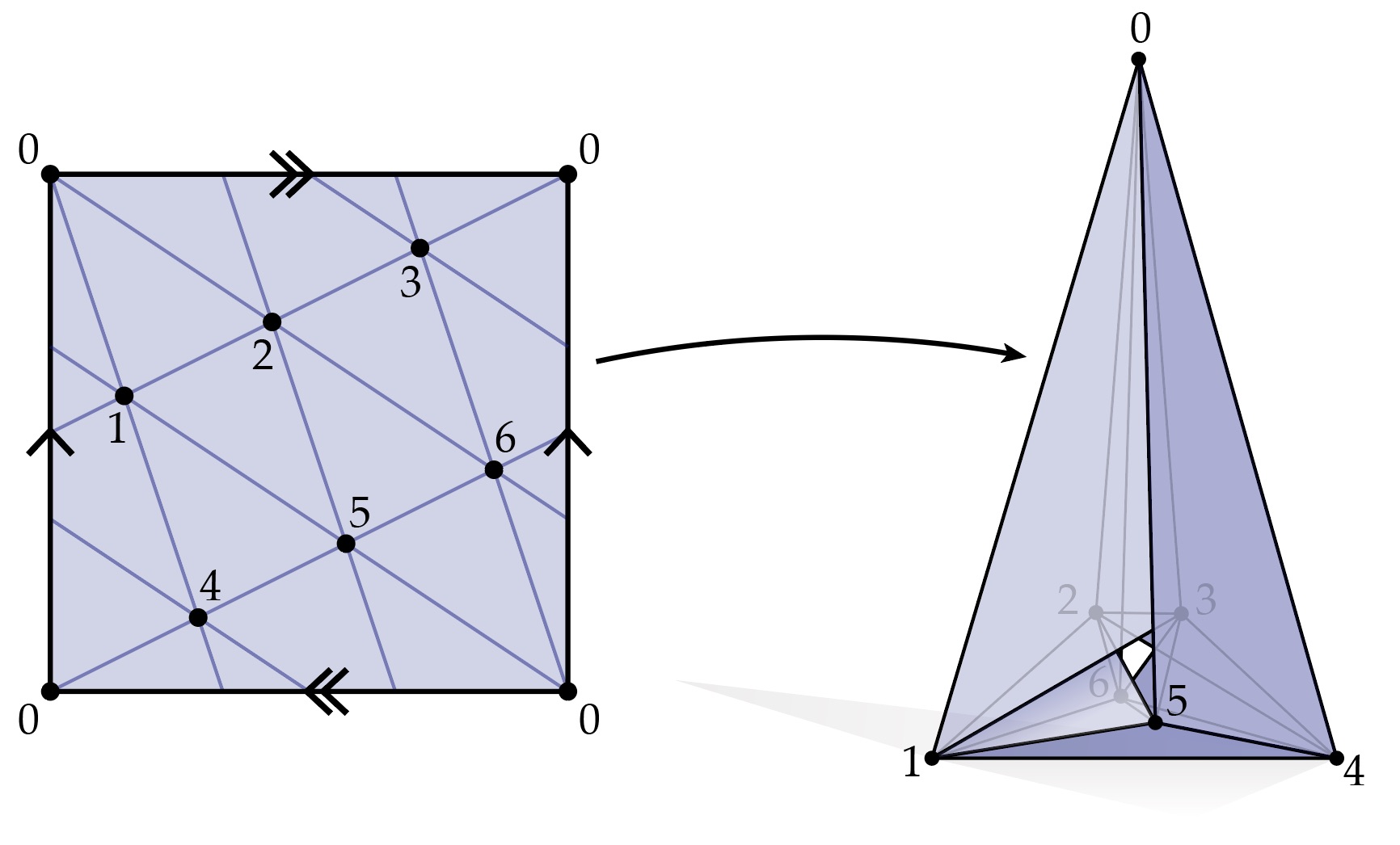
Your next reading will take a dive into purely combinatorial descriptions of surfaces, i.e., those that capture connectivity, but not geometry. These descriptions and data structures will provide the foundation for all the geometry and algorithms we’ll build up in this class. (The reading also provides the essential background for your first written and coding assignments!)
The reading is Chapter 2, pages 7–20 of our course notes, which can always be accessed from the link above.
Your short 2-3 sentence summary is due by 10am Eastern on February 1, 2024. Handin instructions can be found on the assignment page.
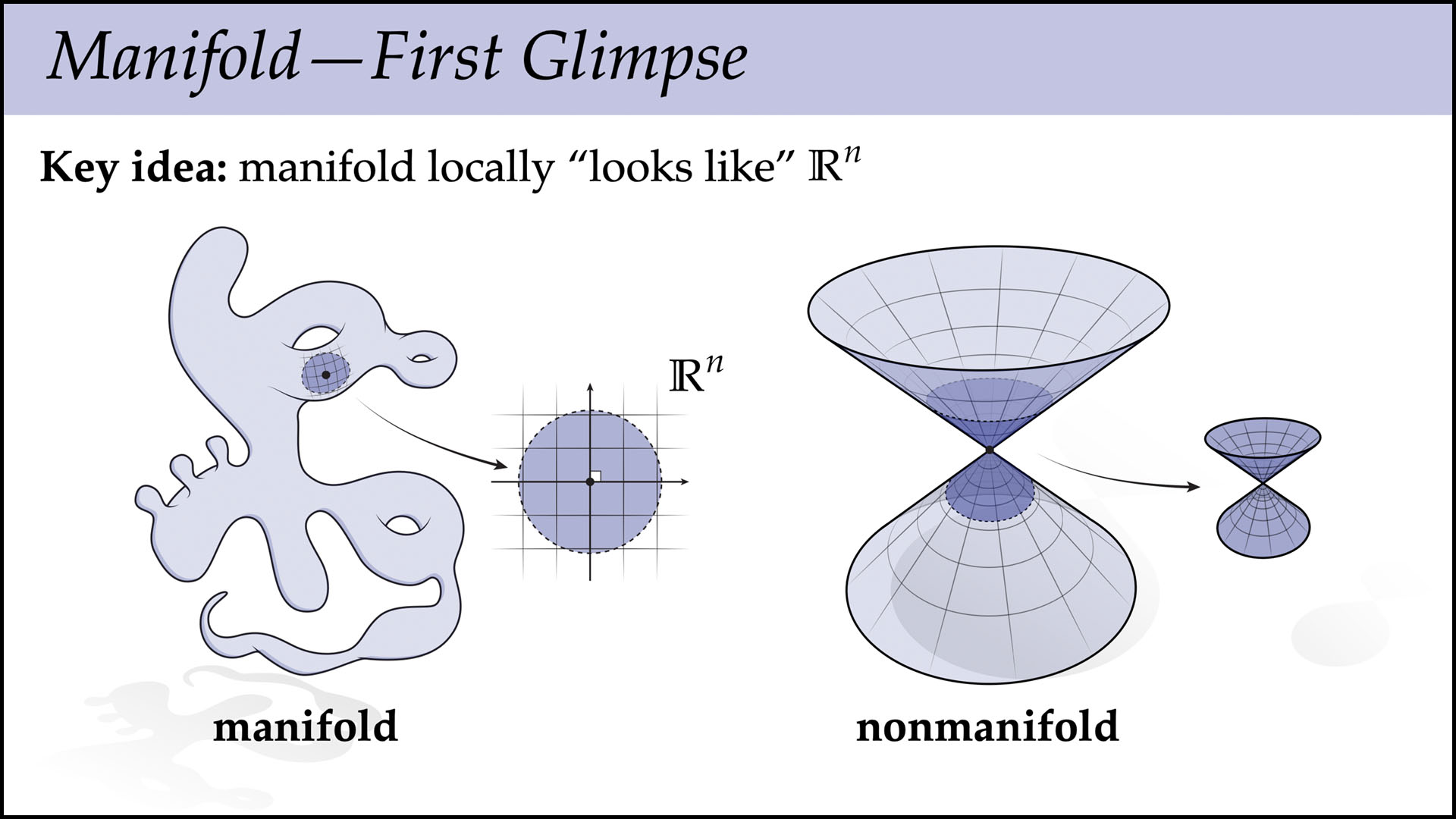
Lecture 2B—Introduction to Manifolds
In this lecture we connect what we learned on the discrete side last time, about combinatorial surfaces and the simplicial complex, to manifolds, which are a central object in differential geometry. Manifolds are, very roughly speaking, a “particularly nice kind of (topological) space,” where concepts like “the neighborhood around a point” are always well-defined, and always look the same. By imposing an additional regularity condition on simplicial complexes, we likewise get a simplicial manifold, which more informally can be thought of as a “particularly nice kind of mesh.” In terms of practical algorithms, it’s often useful to assume manifold input, because it allows you to write code without worrying about tricky special cases.