Your first reading assignment will be to read an overview article on Discrete Differential Geometry. Since we know we have a diverse mix of participants in the class, you have several options (pick one):
- (pages 1–3) Crane & Wardetzky, “A Glimpse into Discrete Differential Geometry”.
This article discusses the “no free lunch” story about curvature we looked at in class, plus a broader overview of the field. - (pages 1–5) Pottman et al, “Architectural Geometry”.
This article discusses the beautiful tale of how discrete differential geometry is linked to modern approaches to computational design for architecture, as well as fabrication and “rationalization” of free-form designs. - (pages 5–9) Bobenko & Suris, “Discrete Differential Geometry: Consistency As Integrability”.
This article provides another overview of discrete differential geometry, with an emphasis on nets and their connection to the notion of integrability in geometry and physics.
Though written for a broad audience, be warned that all of these articles are somewhat advanced—the goal here is not to understand every little detail, but rather just get a high-level sense of what DDG is all about.
Assignment: Pick one of the readings above, and write 2–3 sentences summarizing what you read, plus at least one question about something you didn’t understand, or some thought/idea that occurred to you while reading the article. For this first assignment, we are also very interested to know a little bit about YOU! E.g., why are you taking this course? What’s your background? What do you hope to get out of this course? What are your biggest fears about the course? Etc.
Handin instructions can be found in the “Readings” section of the Assignments page. Note that you must send your summary in no later than 10am Eastern on the day of the next lecture (January 24, 2023).
Enjoy!
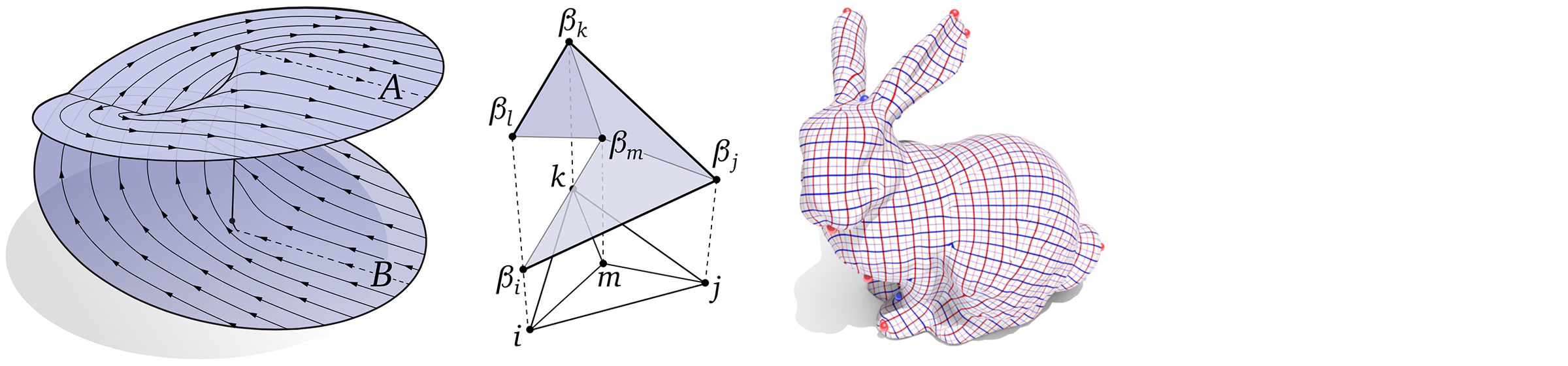
Crane & Wardetzky write that it is well known that movement along normal with magnitude of curvature is the movemvent that changes curvature length most quickly, and I wonder what this claim means. I also wonder how is the osculating circle is determined (circle and radius), both in the smooth and discrete case.