Note: For the final assignment, you can do either this assignment or A5. Overall, you just need to be sure you completed A0 and A1, as well as 3 of the assignments A2–A6 (your choice which ones.) Also, you cannot use late days on this assignment since it’s the last one.
Please implement the following routines in:
- projects/vector-field-decomposition/tree-cotree.[js/cpp]:
- buildPrimalSpanningTree
- inPrimalSpanningTree
- buildDualSpanningCotree
- inDualSpanningCotree
- buildGenerators
- projects/vector-field-decomposition/harmonic-bases.[js/cpp]:
- buildClosedPrimalOneForm
- compute
In addition, please implement either Hodge Decomposition, or Trivial Connections (on surfaces of genus 0):
Hodge Decomposition: Please implement the following routines in
- projects/vector-field-decomposition/hodge-decomposition.[js/cpp]:
- constructor
- computeExactComponent
- computeCoExactComponent
- computeHarmonicComponent
Trivial Connections on Surfaces of Genus 0: Please implement computeConnections in projects/direction-field-design/trivial-connections.[js/cpp]. This file has function signatures for trivial connections on arbitrary surfaces, but for this assignment we are only requiring you to compute the connection form on simply-connected surfaces where you don’t have to worry about the period matrix. You are, of course, welcome to implement the general algorithm if you would like to!
Notes:
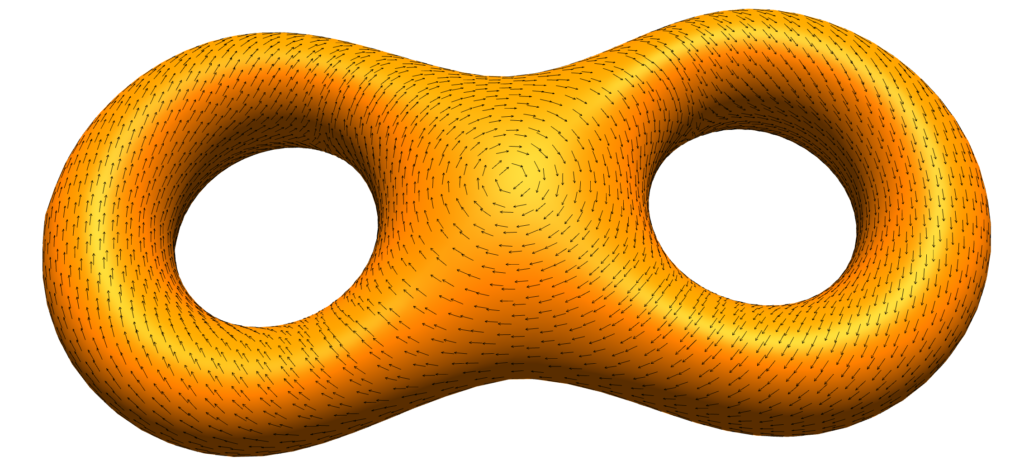
- Recall that homology generators are a set of loops which somehow describe all of the interesting loops on a surface. For example, here are the two homology generators for the torus.
- Your buildGenerators function should implement the Tree-Cotree algorithm, which is Algorithm 5 of section 8.2 of the notes.
- In tree-cotree.[js/cpp] the trees are stored using the dictionaries vertexParent and faceParent. You should store the primal spanning tree by storing the parent of vertex v in vertexParent[v]. The root should be its own parent. Similarly, you should store the dual spanning cotree by storing the parent of face f in faceParent[f].
- The Tree Cotree algorithm finds homology generators on the dual mesh. That is to say, you should take each dual edge which is not in either spanning tree, and form a loop by following its endpoint back up the dual cotree until they meet at the root of the dual cotree. Even though we’re thinking of these homology generators as loops on the dual mesh, we still store them as lists of ordinary halfedges, since edges in the dual mesh are in 1-1 correspondence with edges in the primal graph.
- buildClosedPrimalOneForm should use a homology generator to construct a closed primal 1-form as described in section 8.22 of the notes.
- The compute function in HarmonicBases should compute a harmonic basis using Algorithm 6 in section 8.2 of the notes. If you choose to implement Hodge decomposition for the assignment, you are welcome to use your Hodge decomposition code to solve for $d\alpha$. Otherwise, you can just ignore the hodgeDecomposition parameter and directly solve the linear system $\Delta \alpha = \delta \omega$ to find $\alpha$. (Recall that $\delta$ is the codifferential, which we talked a lot about in the Discrete Exterior Calculus assignment).
Notes (Hodge Decomposition):
- The procedure for Hodge Decomposition is given as Algorithm 3 in section 8.1 of the Notes.
- Note that the SparseMatrix class has an invertDiagonal function that you can use to invert diagonal matrices.
- For computeCoExactComponent, you should compute the coexact component $\delta \beta$ of a differential form $\omega$ by solving the equation $d\delta \beta = d\omega$. As stated in the notes, the most convenient way of doing this is to define a dual 0-form $\tilde \beta := *\beta$, and then to solve $d*d \tilde \beta = d \omega$. Then you can compute $\delta \beta$ using the fact that $\delta \beta = *d*\beta = *d\tilde\beta$. When doing these computations, you should keep tract of whether your forms are primal forms or dual forms, recalling that hodge stars take you from primal forms to dual forms, and hodge star inverses take you from dual forms to primal forms. (THis is discussed in detail in section 8.1.3 of the notes.
- Note that the 2-form Laplacian B is not necessarily positive definite, so you should use an LU solver instead of a Cholesky solver when solving systems involving B.
Notes (Trivial Connections):
- The trivial-connection[-js] file is structured for implementing the full trivial connections algorithm on arbitrary surfaces. Since that’s tricky, we’re only requiring that you compute connections on topological spheres. You should implement this in the computeConnections() function, and it should pass the tests labeled “computeConnections on a sphere”.
- Even though we’re working with spheres, it is still helpful to use the formulation of Trivial connections given in section 8.4.1 of the notes. In particular, you should solve the optimization problem given in Exercise 8.21.
- On a sphere, there are no harmonic 1-forms, so the $\gamma$ part of your Hodge decomposition will always be 0. Furthermore, the sphere has no homology generators, so the problem simplifies to \[\min_{\delta \beta} \;\|\delta\beta\|^2\;\text{s.t.}\; d\delta\beta = u\]
- Following the notes, we observe that the constraint $d\delta\beta = u$ determines $\beta$ up to a constant, and that constant is annihilated by $\delta$. So you can find the connection 1-form $\delta \beta$ with a single linear solve.
Warning: You cannot use late days on this assignment since it’s the last one.
The assignment is due on the date listed on the calendar, at 5:59:59pm Eastern (not at midnight!). Further hand-in instructions can be found on this page.