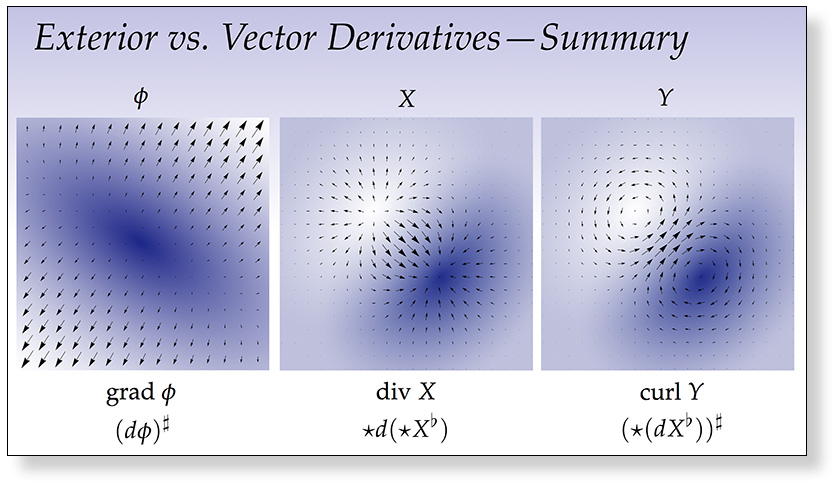
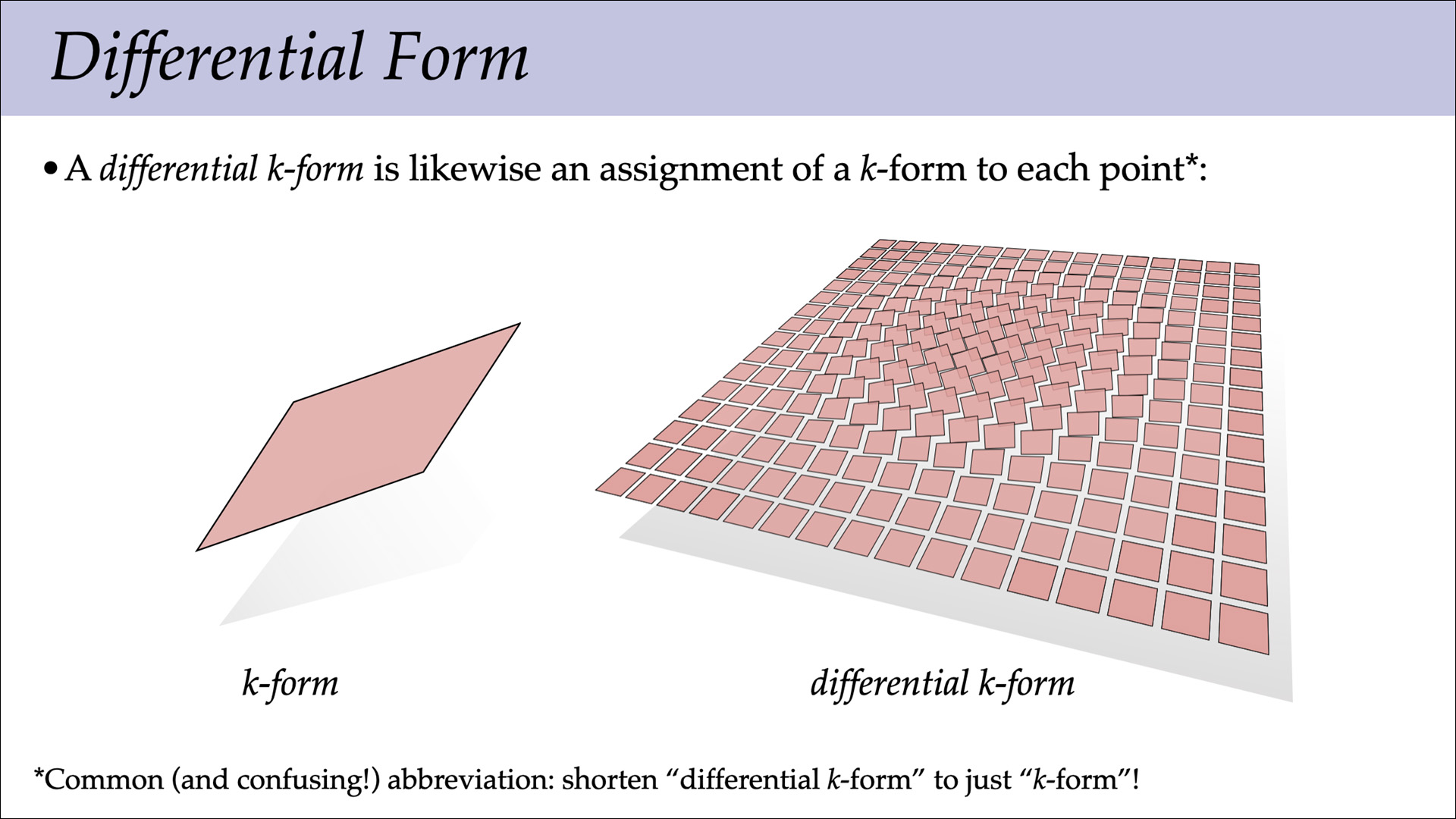
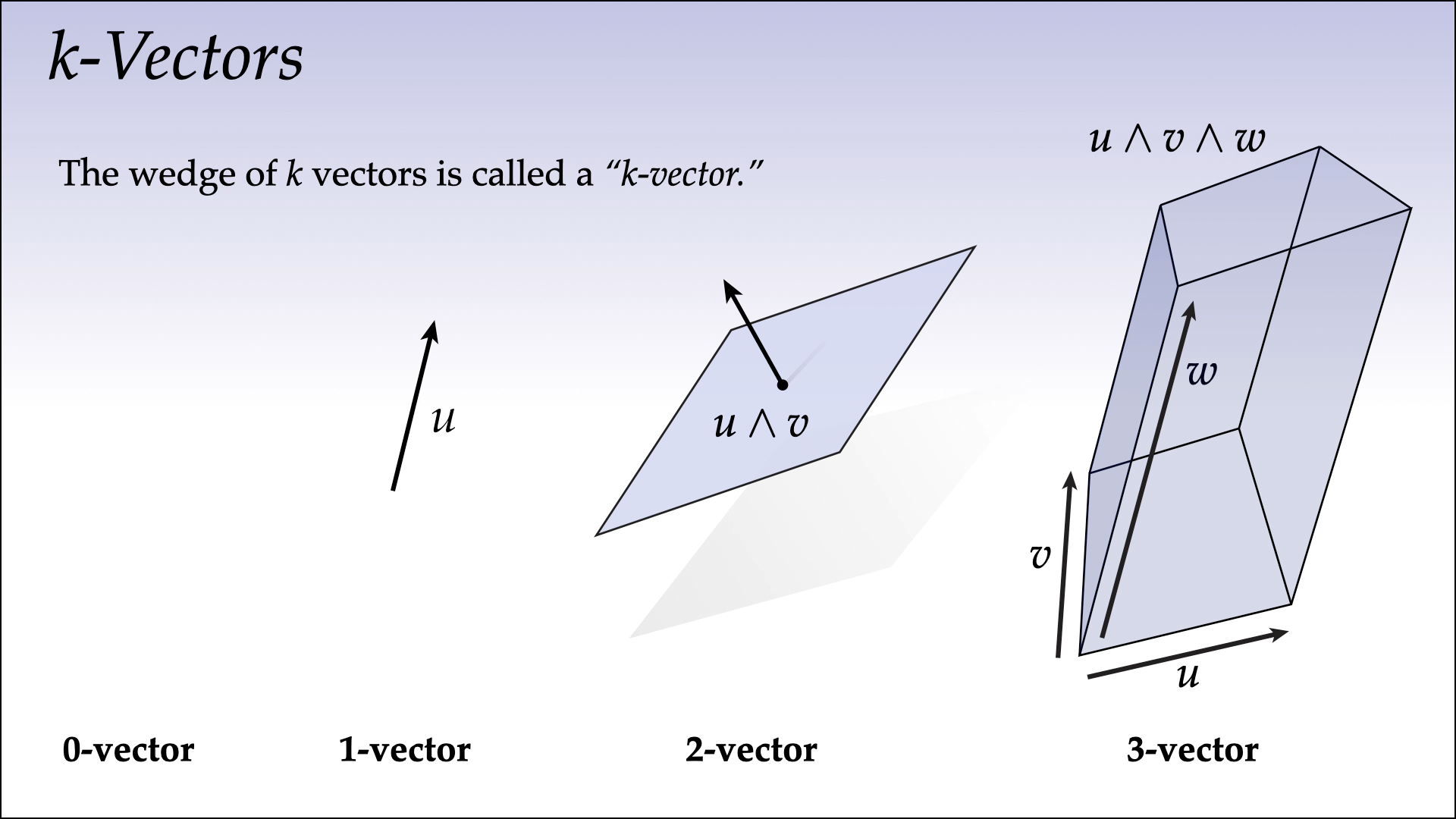
Ordinary calculus provides tools for understanding rates of change (via derivatives), total quantities (via integration), and the total change (via the fundamental theorem of calculus). Exterior calculus generalizes these ideas to \(n\)-dimensional quantities that arise throughout geometry and physics. Our first lecture on exterior calculus studies the exterior derivative, which describes the rate of change of a differential form, and (together with the Hodge star) generalizes the gradient, divergence, and curl operators from standard vector calculus.
Author: Keenan
Assignment 1 (Written): Exterior Calculus (Due 3/18)
The written portion of assignment 1 is now available, which covers some of the fundamental tools we’ll be using in our class. Initially this assignment may look a bit intimidating, but the homework is not as long as it might seem: all the text in the big gray blocks contains supplementary, formal definitions that you do not need to know in order to complete the assignments.
Don’t be shy about asking us questions here in the comments, via email, or during office hours. We want to help you succeed on this assignment, so that you can enjoy all the adventures yet to come…

This assignment is due on Thursday, March 18.
Assignment 1 (Coding): Exterior Calculus (Due 3/18)
![]()
For the coding portion of your first assignment, you will implement the discrete exterior calculus (DEC) operators $\star_0, \star_1, \star_2, d_0$ and $d_1$. Once implemented, you will be able to apply these operators to a scalar function (as depicted above) by pressing the “$\star$” and “$d$” button in the viewer. The diagram shown above will be updated to indicate what kind of differential k-form is currently displayed. These basic operations will be the starting point for many of the algorithms we will implement throughout the rest of the class; the visualization (and implementation!) should help you build further intuition about what these operators mean and how they work
Getting Started
- For this assignment, you need to implement the following routines:
- in core/geometry.[js|cpp]
- cotan
- barycentricDualArea
- in core/discrete-exterior-calculus.[js|cpp]
- buildHodgeStar0Form
- buildHodgeStar1Form
- buildHodgeStar2Form
- buildExteriorDerivative0Form
- buildExteriorDerivative1Form
- in core/geometry.[js|cpp]
In practice, a simple and efficient way to compute the cotangent of the angle $\theta$ between two vectors $u$ and $v$ is to use the cross product and the dot product rather than calling any trigonometric functions directly; we ask that you implement your solution this way. (Hint: how are the dot and cross product of two vectors related to the cosine and sine of the angle between them?)
In case we have not yet covered it in class, the barycentric dual area associated with a vertex $i$ is equal to one-third the area of all triangles $ijk$ touching $i$.
EDIT: You can compute the ratio of dual edge lengths to primal edge lengths using the cotan formula, which can be found on Slide 28 of the Discrete Exterior Calculus lecture, or in exercise 36 of the notes (you don’t have to do the exercise for this homework).
Submission Instructions
Please submit your geometry.[js|cpp] and discrete-exterior-calculus.[js|cpp] files to Gradescope. You should not submit any other source files (and therefore, should not edit any other source files to get your code working!).
Reading 4: Exterior Calculus — due 3/11
The next reading assignment will wrap up our discussion of exterior calculus, both smooth and discrete. In particular, it will explore how to differentiate and integrate \(k\)-forms, and how an important relationship between differentiation and integration (Stokes’ theorem) enables us to turn derivatives into discrete operations on meshes. In particular, the basic data we will work with in the computational setting are “integrals of derivatives,” which amount to simple scalar quantities we can associate with the vertices, edges, faces, etc. of a simplicial mesh. These tools will provide the basis for the algorithms we’ll explore throughout the rest of the semester.
The reading is the remainder of Chapter 4 from the course notes, “A Quick and Dirty Introduction to Exterior Calculus”, Sections 4.6 through 4.8 (pages 67–83). Note that you just have to read these sections; you do not have to do the written exercises; a different set of written problems will be posted later on. The reading is due Thursday, March 11 at 10am. See the assignments page for handin instructions.
Lecture 5: Differential Forms
Lecture 4: \(k\)-Forms
Today we continue our journey toward building up (discrete) exterior calculus by talking about how to measure little k-dimensional volumes. Just like rulers measure length, and cups measure volume, k-forms will be used to take measurements of the little k-dimensional volumes or k-vectors that we built up using exterior algebra in our previous lecture. Such measurements will ultimately allow us to talk about integration over curved spaces; in the discrete setting, these measurements will be the basic data we associate with the elements of mesh.
Reading 3: Exterior Algebra and k-Forms (due 3/2)
Your next reading assignment will help you review the concepts we’ve been discussing in class: describing “little volumes” or \(k\)-vectors using the wedge product and the Hodge star, and measuring these volumes using “dual” volumes called \(k\)-forms. These objects will ultimately let us integrate quantities over curved domains, which will also be our main tool for turning smooth equations from geometry and physics into discrete equations that we can actually solve on a computer.
The reading is Chapter 4, “A Quick and Dirty Introduction to Exterior Calculus”, up through section 4.5.1 (pages 45–65). It will be due Tuesday, March 2 at 10am Eastern time. See the assignments page for handin instructions.
Your next homework will give you some hands-on practice with differential forms; just take this time to get familiar with the basic concepts.
Lecture 3: Exterior Algebra
Our next lecture will cover one of the basic tools we’ll use throughout the rest of the course: exterior algebra. The basic idea is to add a couple new operations to our usual list of vector operations (dot product, cross product, etc.) that make it easy to talk about volumes rather than just vectors. If you felt ok working with things like the cross product and the determinant in your linear algebra/vector calculus courses, this shouldn’t be too big of a leap. (If not, could be a good moment for a review!)
Lecture 2B: Introduction to Manifolds
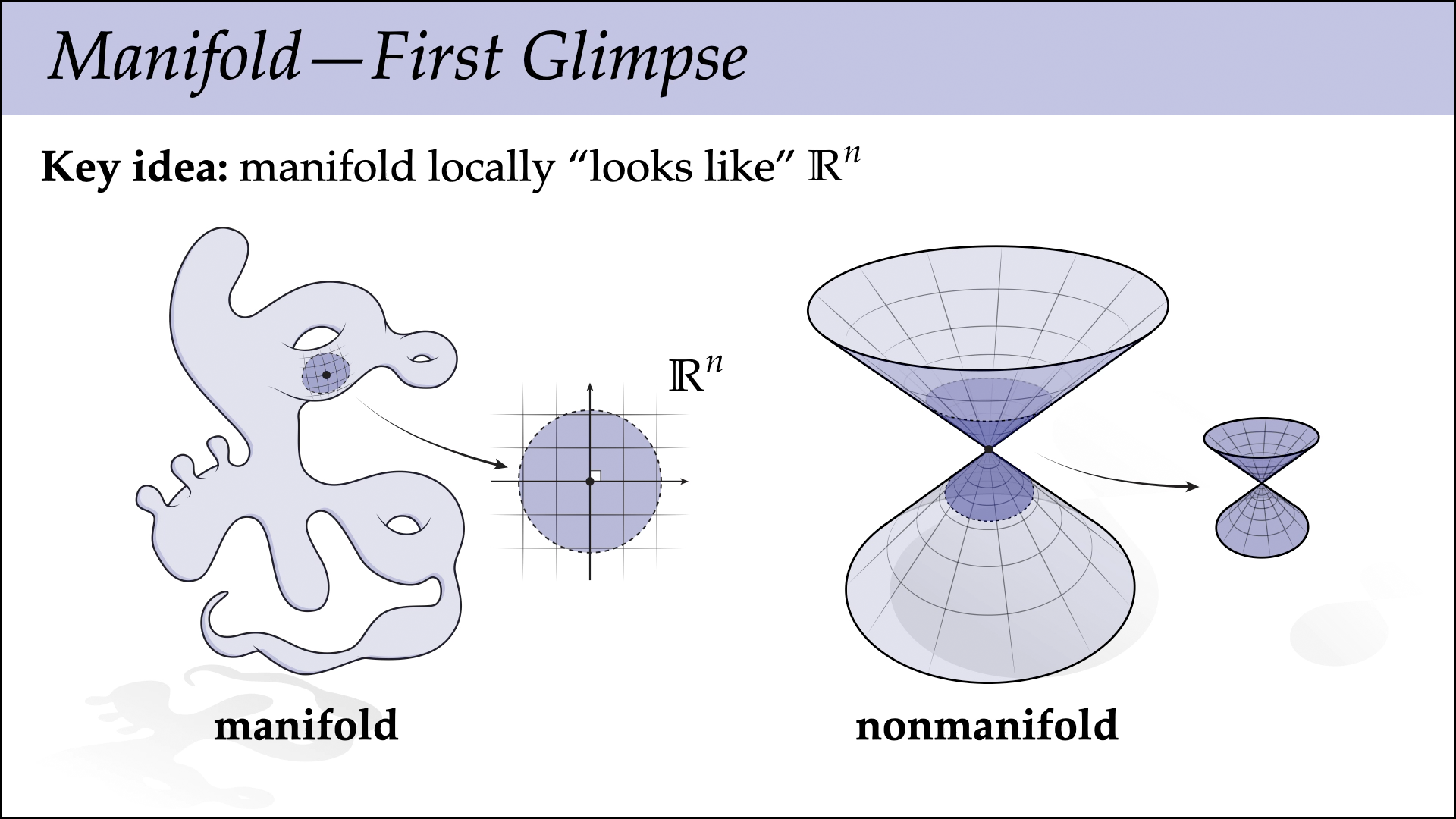
In tomorrow’s lecture we will catch a first glimpse of the idea of manifolds, which are pretty central to differential geometry. Rather than giving a formal definition in the smooth case, we’ll introduce a notion of discrete manifolds that capture the most important ideas. These discrete manifolds build on the idea of a simplicial complex, introduced in the previous lecture.
Reading 2: Combinatorial Surfaces (Due 2/19)

Your next reading will take a dive into purely combinatorial descriptions of surfaces, i.e., those that capture connectivity, but not geometry. These descriptions and data structures will provide the foundation for all the geometry and algorithms we’ll build up in this class. (The reading also provides the essential background for your first written and coding assignments!)
The reading is Chapter 2, pages 7–20 of our course notes, which can always be accessed from the link above.
Your short 2-3 sentence summary is due by 10am Eastern on February 19, 2020. Handin instructions can be found on the assignment page.