This lecture presents the discrete counterpart of the previous lecture on smooth curves. Here we also arrive at a discrete version of the fundamental theorem for plane curves: a discrete curve is completely determined by its discrete parameterization (a.k.a. edge lengths) and its discrete curvature (a.k.a. exterior angles). Can you come up with a discrete version of the fundamental theorem for space curves? If we think of torsion as the rate at which the binormal is changing, then a natural analogue might be to (i) associate a binormal \(B_i\) with each vertex, equal to the normal of the plane containing \(f_{i-1}\), \(f_{i}\), and \(f_{i+1}\), and (ii) associate a torsion \(\tau_{ij}\) to each edge \(ij\), equal to the angle between \(B_i\) and \(B_{i+1}\). Using this data, can you recover a discrete space curve from edge lengths \(\ell_{ij}\), exterior angles \(\kappa_i\) at vertices, and torsions \(\tau_{ij}\) associated with edges? What’s the actual algorithm? (If you find this problem intriguing, leave a comment in the notes! It’s not required for class credit.)
Author: Keenan
Lecture 10—Smooth Curves
After spending a great deal of time understanding some basic algebraic and analytic tools (exterior algebra and exterior calculus), we’ll finally start talking about geometry in earnest, starting with smooth plane and space curves. Even low-dimensional geometry like curves reveal a lot of the phenomena that arise when studying curved manifolds in general. Our main result for this lecture is the fundamental theorem of space curves, which reveals that (loosely speaking) a curve is entirely determined by its curvatures. Descriptions of geometry in terms of “auxiliary” quantities such as curvature play an important role in computation, since different algorithms may be easier or harder to formulate depending on the quantities or variables used to represent the geometry. Next lecture, for instance, we’ll see some examples of algorithms for curvature flow, which naturally play well with representations based on curvature!
Slides—Discrete Exterior Calculus
This lecture wraps up our discussion of discrete exterior calculus, which will provide the basis for many of the algorithms we’ll develop in this class. Here we’ll encounter the same operations as in the smooth setting (Hodge star, wedge product, exterior derivative, etc.), which in the discrete setting are encoded by simple matrices that translate problems involving differential forms into ordinary linear algebra problems.
Slides—Discrete Differential Forms
In this lecture, we turn smooth differential \(k\)-forms into discrete objects that we can actually compute with. The basic idea is actually quite simple: to capture some information about a differential \(k\)-form, we integrate it over each oriented \(k\)-simplex of a mesh. The resulting values are just ordinary numbers that give us some sense of what the original \(k\)-form must have looked like.
Slides—Exterior Calculus II: Integration
Our first lecture on exterior calculus covered differentiation; our second lecture completes the picture by discussing integration of differential forms. The relationship between integration and differentiation is encapsulated by Stokes’ theorem, which generalizes the fundamental theorem of calculus, as well as many other important theorems from vector calculus and complex analysis (divergence theorem, Green’s theorem, Cauchy’s integral formula, etc.). Stokes’ theorem also plays a key role in numerical discretization of geometric problems, appearing for instance in finite volume methods and boundary element methods; for us it will be the essential tool for developing a discrete version of differential forms that we can actually compute with.
Slides—Exterior Calculus I: Differentiation
Ordinary calculus provides tools for understanding rates of change (via derivatives), total quantities (via integration), and the total change (via the fundamental theorem of calculus). Exterior calculus generalizes these ideas to \(n\)-dimensional quantities that arise throughout geometry and physics. Our first lecture on exterior calculus studies the exterior derivative, which describes the rate of change of a differential form, and (together with the Hodge star) generalizes the gradient, divergence, and curl operators from standard vector calculus.
Slides—Differential Forms in \(R^n\)
A differential \(k\)-form describes a \(k\)-dimensional measurement at each point of space. For instance, the area 2-form on a sphere tells us how much each little piece of the sphere should contribute to an integral over the sphere. In this lecture we give some basic facts and definitions about differential \(k\)-forms, and how to work with them in coordinates. Ultimately differential \(k\)-forms will pave the way to a general notion of integration, which in turn will be our basic mechanism for turning smooth equations into discrete ones (by integrating over elements of a mesh).
Reading 2: Combinatorial Surfaces
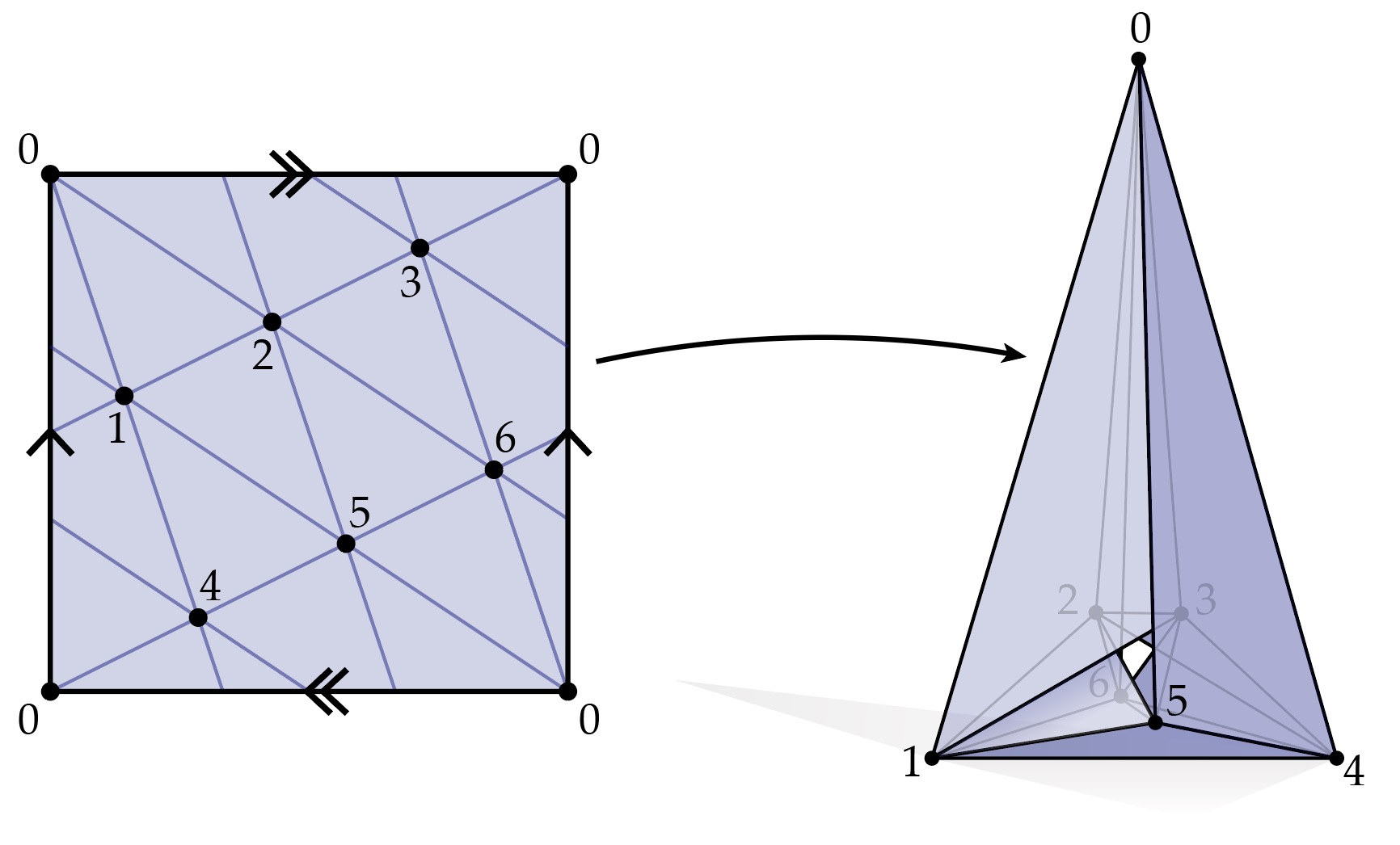
Your next reading will take a dive into purely combinatorial descriptions of surfaces, i.e., those that capture connectivity, but not geometry. These descriptions and data structures will provide the foundation for all the geometry and algorithms we’ll build up in this class. (The reading also provides the essential background for your first written and coding assignments!)
The reading is Chapter 2, pages 7–20 of our course notes, which can always be accessed from the link above.
Your short 2-3 sentence summary is due by 10am Eastern on February 2, 2023. Handin instructions can be found on the assignment page.
Slides—\(k\)-Forms
Today we continue our journey toward building up (discrete) exterior calculus by talking about how to measure little k-dimensional volumes. Just like rulers measure length, and cups measure volume, k-forms will be used to take measurements of the little k-dimensional volumes or k-vectors that we built up using exterior algebra in our previous lecture. Such measurements will ultimately allow us to talk about integration over curved spaces; in the discrete setting, these measurements will be the basic data we associate with the elements of mesh.
Assignment 0 (Coding): Combinatorial Surfaces

For the coding portion of your first assignment, you will implement some operations on simplicial complexes which were discussed in class and in Chapter 2 of the course notes. Once implemented, you will be able to select simplices and apply these operations to them by clicking the appropriate buttons in the viewer (shown above).
Getting Started
- Decide whether you want to use the web skeleton (in JavaScript) or the desktop skeleton (in C++). The web skeleton should “just work” for anyone with a web browser. Setting up the C++ skeleton is also fairly automatic (just a few git commands), but requires a little more familiarity with coding environments. (The benefit of the C++ version is that it’s built on a richer, real-world mesh processing/visualization library than the web version.)
- To use the JavaScript version, download or clone the files in the ddg-exercises-js repository.
- To use the C++ version, follow the instructions in the ddg-exercises repository. It is important that you follow the “Getting Started” instructions and do not simply git clone the repo. Otherwise, dependencies will not be installed correctly, and the code will not build. If you struggle to get the C++ version working on your platform, we recommend you switch to the JavaScript version.
- Either way, you should need to download just one code skeleton for the whole semester (though we may push periodic updates to fix bugs, etc.).
- For this assignment, you will need to implement the following routines in projects/simplicial-complex-operators/simplicial-complex-operators.[js|cpp]:
- assignElementIndices
- buildVertexEdgeAdjacencyMatrix
- buildEdgeFaceAdjacencyMatrix
- buildVertexVector
- buildEdgeVector
- buildFaceVector
- star
- closure
- link
- isComplex
- isPureComplex
- boundary
Notes
- The JavaScript assignment comes with a viewer projects/simplicial-complex-operators/index.html which lets you apply your operators to simplices of meshes and visualize the results. Likewise, the C++ version comes with a viewer with similar functionality. (Viewers will be available for all assignments throughout the semester.)
- Pay close attention to the course notes! Some routines really must be implemented with sparse matrices, not directly with the halfedge mesh data structure.
- Selecting simplices will not work until you fill in the assignElementIndices function.
- The assignment also comes with a test script tests/simplicial-complex-operators/text.html which you can use to verify the correctness of your operators.
- The web framework is implemented in Javascript, which means no compilation or installation is necessary on any platform. You can simply get started by opening the index.html file in projects/discrete-exterior-calculus/ in a web browser. We recommend using Chrome or Firefox. Safari has poor WebGL performance.
- If you do not have prior experience with Javascript, do not worry! You should be able to get a handle on Javascript syntax by reading through some of the code in the framework (a good place to start might be core/geometry.js). The framework also contains extensive documentation (see docs/index.html).
- All browsers come with tools for debugging (for instance the JavaScript Console in Chrome).
Submission Instructions
The assignment is due on the date listed on the calendar, at 5:59:59pm Eastern (not at midnight!). Further hand-in instructions can be found on this page.