This lecture wraps up our discussion of discrete exterior calculus, which will provide the basis for many of the algorithms we’ll develop in this class. Here we’ll encounter the same operations as in the smooth setting (Hodge star, wedge product, exterior derivative, etc.), which in the discrete setting are encoded by simple matrices that translate problems involving differential forms into ordinary linear algebra problems.
Category: Slides
Slides—Discrete Differential Forms
In this lecture, we turn smooth differential \(k\)-forms into discrete objects that we can actually compute with. The basic idea is actually quite simple: to capture some information about a differential \(k\)-form, we integrate it over each oriented \(k\)-simplex of a mesh. The resulting values are just ordinary numbers that give us some sense of what the original \(k\)-form must have looked like.
Slides—Exterior Calculus II: Integration
Our first lecture on exterior calculus covered differentiation; our second lecture completes the picture by discussing integration of differential forms. The relationship between integration and differentiation is encapsulated by Stokes’ theorem, which generalizes the fundamental theorem of calculus, as well as many other important theorems from vector calculus and complex analysis (divergence theorem, Green’s theorem, Cauchy’s integral formula, etc.). Stokes’ theorem also plays a key role in numerical discretization of geometric problems, appearing for instance in finite volume methods and boundary element methods; for us it will be the essential tool for developing a discrete version of differential forms that we can actually compute with.
Slides—Exterior Calculus I: Differentiation
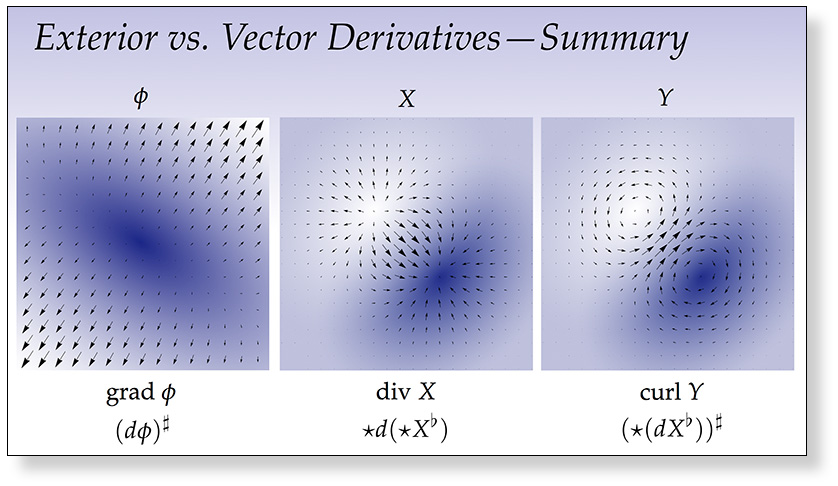
Ordinary calculus provides tools for understanding rates of change (via derivatives), total quantities (via integration), and the total change (via the fundamental theorem of calculus). Exterior calculus generalizes these ideas to \(n\)-dimensional quantities that arise throughout geometry and physics. Our first lecture on exterior calculus studies the exterior derivative, which describes the rate of change of a differential form, and (together with the Hodge star) generalizes the gradient, divergence, and curl operators from standard vector calculus.
Slides—Differential Forms in \(R^n\)
A differential \(k\)-form describes a \(k\)-dimensional measurement at each point of space. For instance, the area 2-form on a sphere tells us how much each little piece of the sphere should contribute to an integral over the sphere. In this lecture we give some basic facts and definitions about differential \(k\)-forms, and how to work with them in coordinates. Ultimately differential \(k\)-forms will pave the way to a general notion of integration, which in turn will be our basic mechanism for turning smooth equations into discrete ones (by integrating over elements of a mesh).
Slides—\(k\)-Forms
Today we continue our journey toward building up (discrete) exterior calculus by talking about how to measure little k-dimensional volumes. Just like rulers measure length, and cups measure volume, k-forms will be used to take measurements of the little k-dimensional volumes or k-vectors that we built up using exterior algebra in our previous lecture. Such measurements will ultimately allow us to talk about integration over curved spaces; in the discrete setting, these measurements will be the basic data we associate with the elements of mesh.
Recitation: Getting started with the coding assignments
Here is a nice recording of the recitation session from earlier years.
This serves as a review on the halfedge data structure, working with sparse matrices and solving linear systems.
Full video and slides are available here:
- Full video
- Concept review (0:00 – 16:58)
- Intro to ddg-exercises-js (16:58 – 23:22)
- Intro to ddg-exercises (C++) (23:22 – 31:41)
- Slides
Slides—Exterior Algebra
Today’s lecture will cover one of the basic tools we’ll use throughout the rest of the course: exterior algebra. The basic idea is to add a couple new operations to our usual list of vector operations (dot product, cross product, etc.) that make it easy to talk about volumes rather than just vectors. If you felt ok working with things like the cross product and the determinant in your linear algebra/vector calculus courses, this shouldn’t be too big of a leap. (If not, could be a good moment for a review!)
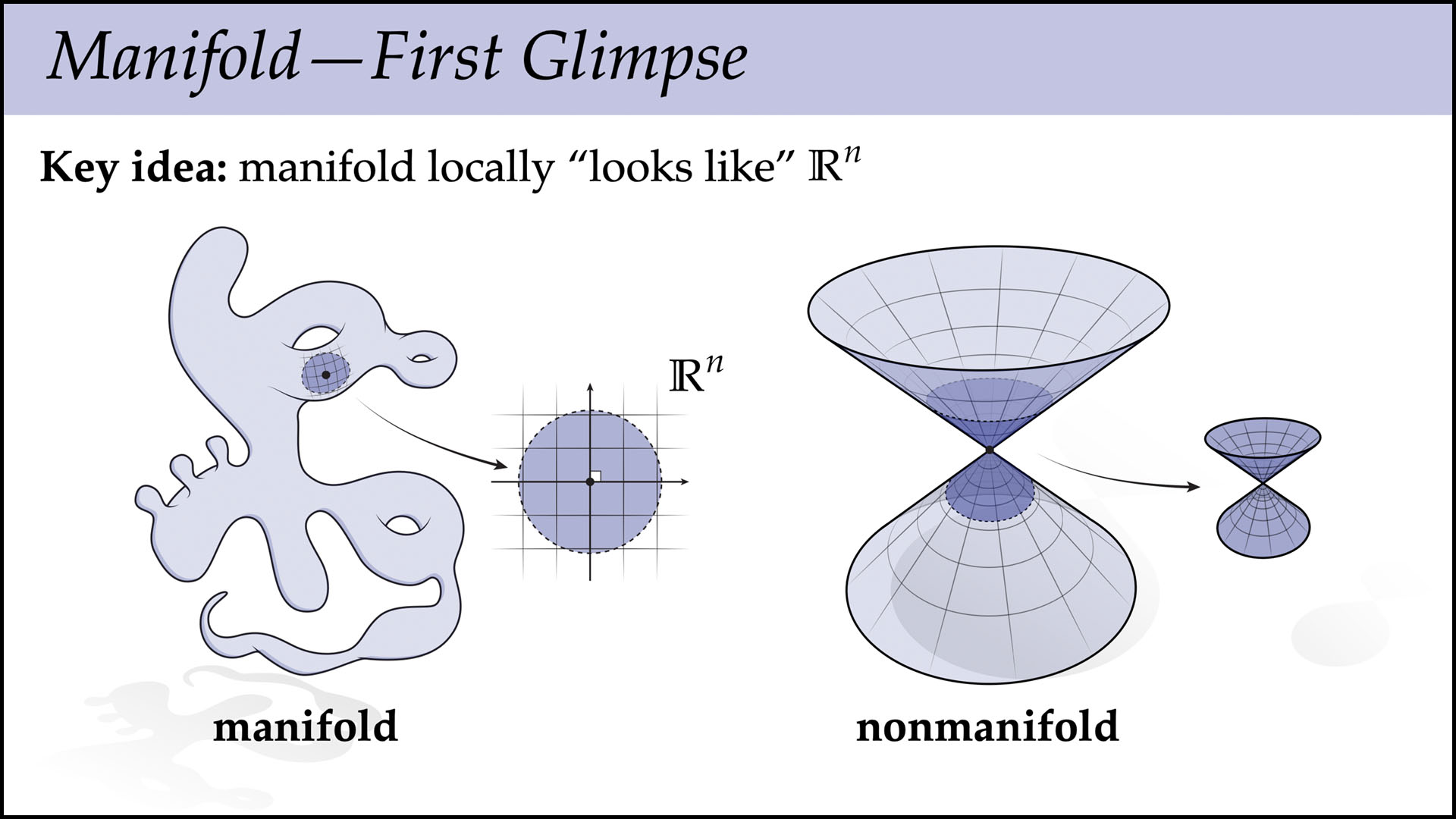
Lecture 2B—Introduction to Manifolds
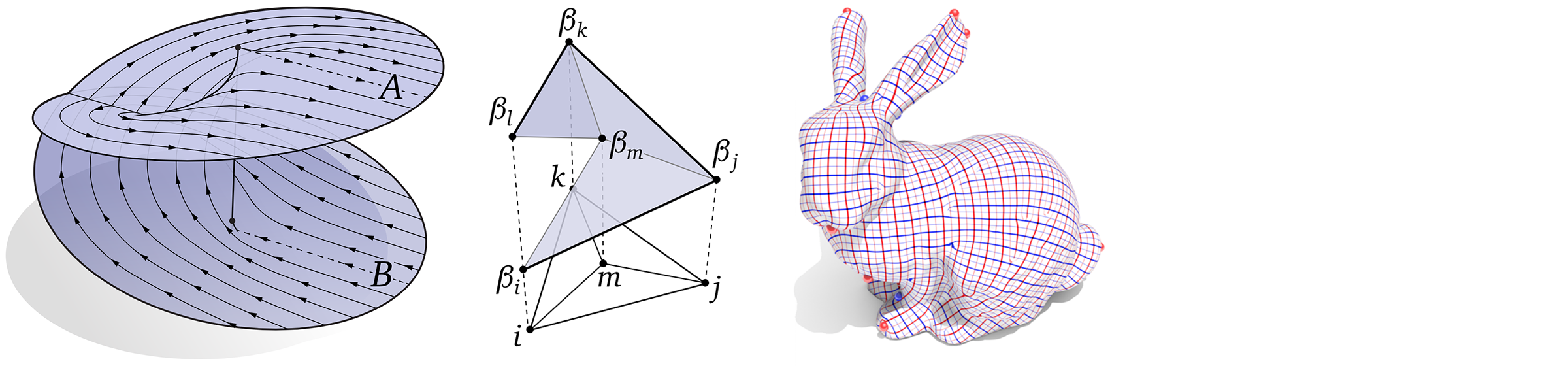
In this lecture we connect what we learned on the discrete side last time, about combinatorial surfaces and the simplicial complex, to manifolds, which are a central object in differential geometry. Manifolds are, very roughly speaking, a “particularly nice kind of (topological) space,” where concepts like “the neighborhood around a point” are always well-defined, and always look the same. By imposing an additional regularity condition on simplicial complexes, we likewise get a simplicial manifold, which more informally can be thought of as a “particularly nice kind of mesh.” In terms of practical algorithms, it’s often useful to assume manifold input, because it allows you to write code without worrying about tricky special cases.
Lecture 2—Combinatorial Surfaces
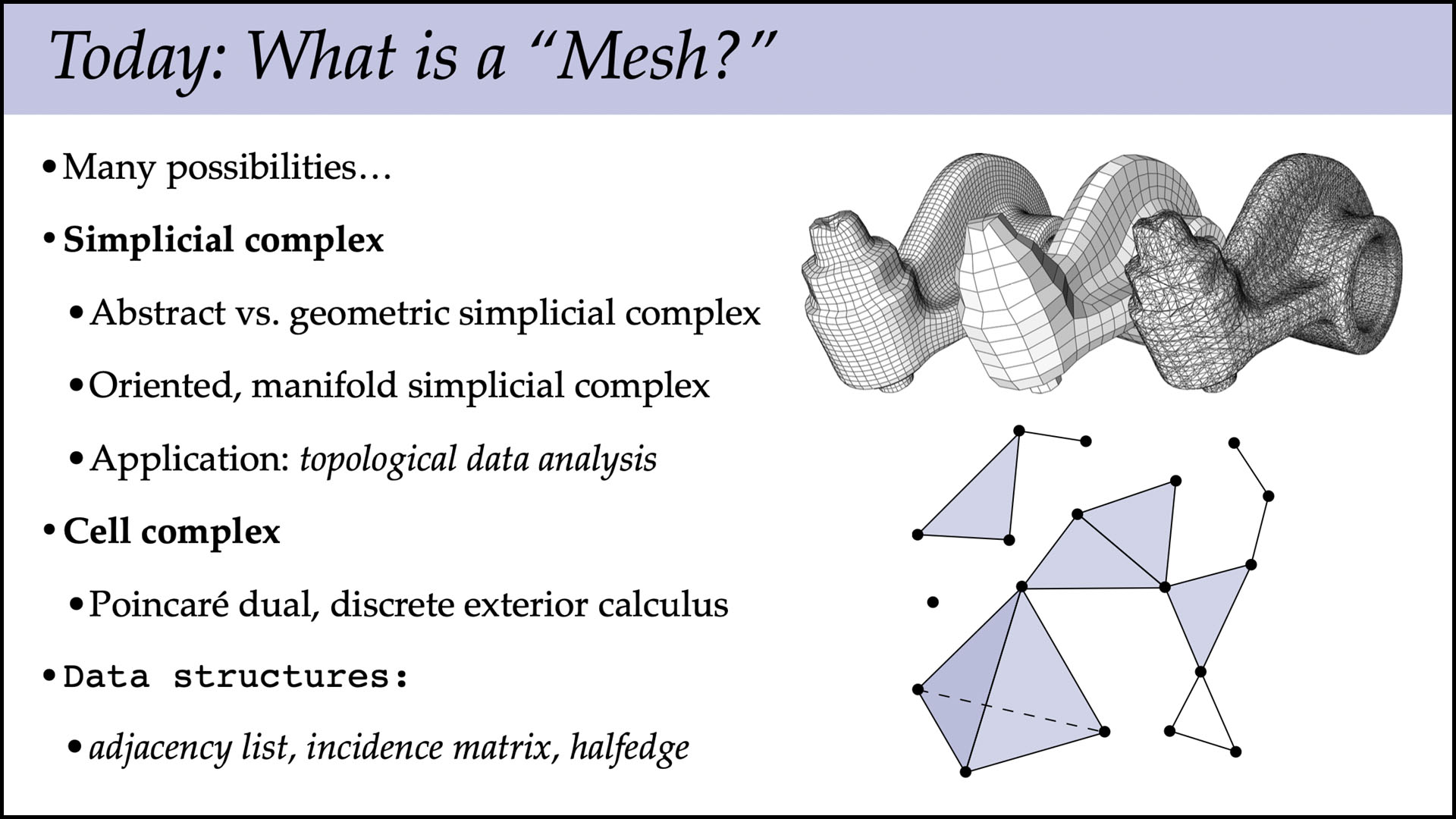
This lecture gives one precise definition to the notion of a “mesh,” namely a simplicial complex. If we consider only the connectivity of a simplicial complex, rather than any locations for its vertices in space, we get an abstract simplicial complex. From the perspective of differential geometry, an abstract simplicial complex plays the role of a so-called topological space, telling us how the domain is “connected up,” without saying anything specific about its geometry.